[논문] DoRA: Weight-Decomposed Low-Rank Adaptation

ABSTRACT

많이 사용되는 파라미터 효율적인 미세조정(Parameter-Efficient Fine-Tuning, PEFT) 방법 중, LoRA와 그 변형들이 추가적인 추론 비용을 피하면서 상당한 인기를 얻고 있다. 그러나 이러한 방법들과 완전 미세조정(Full Fine-Tuning, FT) 사이에는 여전히 종종 정확도 격차가 존재한다.

이 연구에서는 먼저, FT와 LoRA 간의 본질적인 차이를 조사하기 위해 새로운 가중치 분해 분석(Weight Decomposition Analysis)을 소개한다. 이 분석 결과를 바탕으로 FT의 학습 능력을 유사하게 구현하기 위해, 우리는 Weight-Decomposed Low-Rank Adaptation (DoRA)을 제안한다. DoRA는 사전 학습된 가중치를 크기(Magnitude)와 방향(Direction)이라는 두 가지 구성 요소로 분해하여 미세조정을 수행하며, 특히 방향 업데이트에 LoRA를 사용하여 학습 가능한 파라미터 수를 효율적으로 최소화한다.

DoRA는 LoRA의 학습 능력과 학습 안정성을 모두 향상시키면서도 추가적인 추론 오버헤드를 피한다. DoRA는 commonsense reasoning, visual instruction tuning, image/video-text understanding 등의 다양한 다운스트림 작업에서 LLaMA, LLaVA, VL-BART를 미세조정할 때 LoRA보다 일관되게 더 나은 성능을 보인다. 코드는 https://github.com/NVlabs/DoRA에서 제공된다.

 

1. Introduction

사전 학습된 모델들은 NLP와 다중 모달 작업 등에서 뛰어난 일반화 능력을 보여준다. 하지만 모델 크기가 커지면서 완전 미세조정(FT)은 비용이 크게 증가한다. 이를 해결하기 위해, 최소한의 파라미터로 미세조정하는 PEFT 방법들이 제안되었으며, 그중 LoRA는 단순성과 효율성으로 주목받고 있다. 그러나 LoRA는 FT와 비교해 학습 능력에서 차이가 있으며, 이는 주로 제한된 파라미터 수 때문이라고 여겨졌다.

이 연구에서는 가중치 분해 분석을 통해 LoRA와 FT의 학습 차이를 조사한다. LoRA와 FT는 각기 다른 업데이트 패턴을 보이며, 이러한 차이가 학습 능력의 차이를 설명한다고 본다. 이를 바탕으로, 우리는 새로운 PEFT 방법인 DoRA를 제안한다. DoRA는 사전 학습된 가중치를 크기(Magnitude)와 방향(Direction)으로 나눠 조정하며, 방향 업데이트에 LoRA를 사용해 효율성을 유지한다.

DoRA의 overview

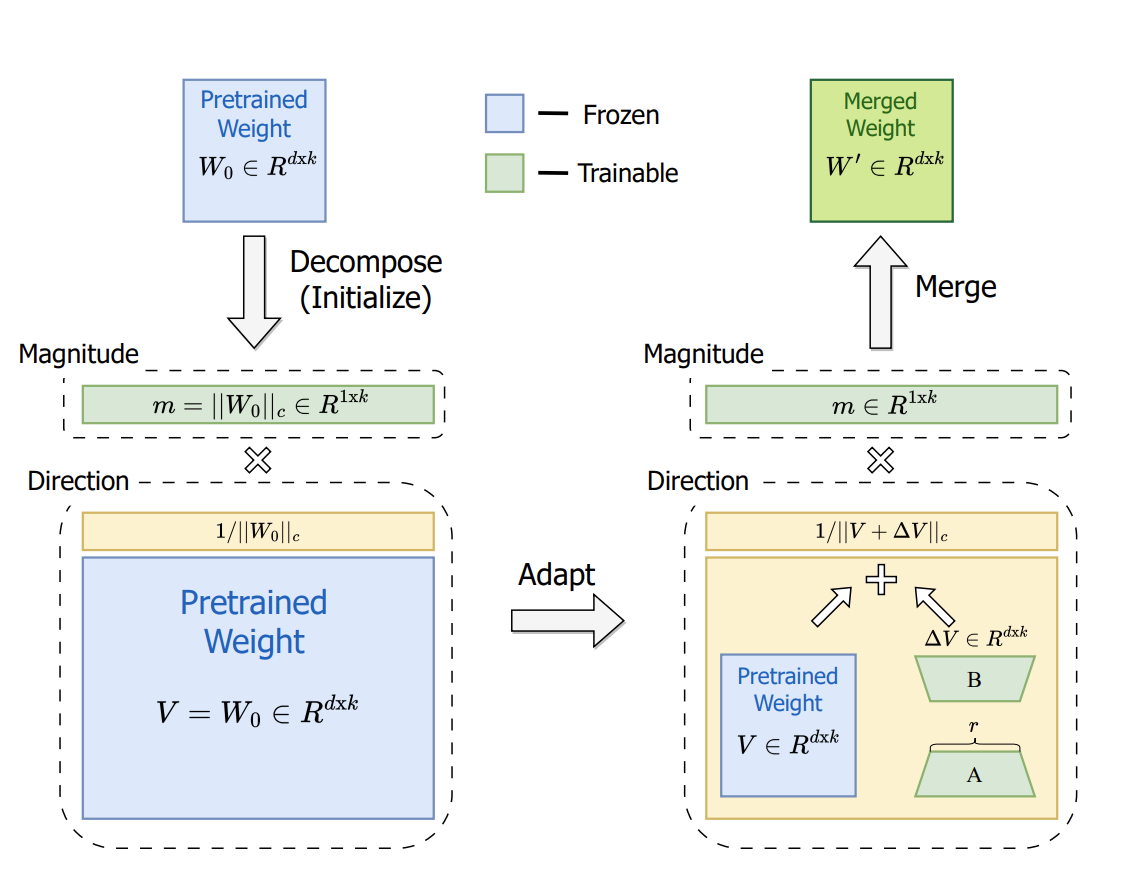
DoRA는 실험적으로 FT와 유사한 학습 능력을 가지면서도, LoRA보다 다양한 작업(NLP, 비전-언어 등)에서 더 높은 성능을 보였다. 특히 LLaMA, LLaVA, VL-BART 등의 다양한 모델에서 LoRA를 능가하는 결과를 기록했다. DoRA는 추가적인 추론 비용 없이 FT와 비슷한 학습 효과를 제공한다는 점에서 PEFT의 새로운 가능성을 제시한다.

 

2. Related Works

PEFT(파라미터 효율적인 미세조정) 방법은 대규모 모델의 미세조정 비용을 줄이기 위해 전체 파라미터 중 일부만 학습한다. 기존 PEFT 방법은 세 가지로 나뉜다.

1. 어댑터 기반 방법(Adapter-based methods)
   모델에 추가 학습 모듈을 도입해 성능을 개선하는 방법으로, 기존 레이어에 직렬 또는 병렬로 선형 모듈을 추가한다(Houlsby et al., 2019; He et al., 2021).
   단점: 모델 아키텍처를 변경해 추론 지연이 증가한다.
2. 프롬프트 기반 방법(Prompt-based methods)
   입력에 학습 가능한 소프트 토큰(프롬프트)을 추가하여 이를 미세조정하는 방법이다(Lester et al., 2021).
   단점: 초기화 민감도로 인해 효과가 제한된다.
3. LoRA와 그 변형
   LoRA는 저차원 행렬로 가중치 변화를 근사하여 학습하며, 추론 시 사전 학습된 가중치와 병합되므로 추가적인 추론 부담이 없다(Hu et al., 2022).
   예: SVD 분해(Zhang et al., 2023), Hadamard 곱(Hyeon-Woo et al., 2022), 정규 행렬 분해(Qiu et al., 2023) 등을 활용한 방식.

이 연구는 LoRA와 같은 세 번째 범주에 속하며, LoRA 및 그 변형들과의 비교를 통해 제안 방법의 효과를 입증한다.

 

3. Pattern Analysis of LoRA and FT

3.1. Low-Rank Adaptation (LoRA)

LoRA(Hu et al., 2022)는 미세조정 동안 발생하는 업데이트가 낮은 "내재적 랭크(intrinsic rank)"를 가진다는 가설에 기반하여, 두 개의 저랭크 행렬의 곱을 이용해 사전 학습된 가중치를 점진적으로 업데이트할 것을 제안한다.
사전 학습된 가중치 행렬 W0∈Rd×k에 대해, LoRA는 가중치 업데이트 ΔW∈Rd×k를 저랭크 분해 방식인 BA로 표현한다. 따라서, 미세조정된 가중치 W′W'는 다음과 같이 표현할 수 있다:

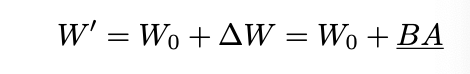
여기서 W0는 미세조정 과정 동안 고정되고, B와 A가 학습된다. 행렬 AA는 Kaiming 균등 분포(He et al., 2015)로 초기화되며, BB는 0으로 초기화된다. 따라서 학습 시작 시점에서 ΔW=BA는 0이다. W′와 W0가 모두 Rd×k의 차원을 가지므로, LoRA와 관련 변형은 원래 모델에 비해 추론 시 추가적인 지연을 초래하지 않는다.

3.2. Weight Decomposition Analysis

LoRA(Hu et al., 2022)의 연구는 LoRA가 완전 미세조정(Full Fine-Tuning, FT)의 일반적인 근사로 간주될 수 있음을 시사한다. LoRA의 랭크 rr를 점진적으로 증가시켜 사전 학습된 가중치의 랭크와 일치시킴으로써, LoRA는 FT와 유사한 표현력을 얻을 수 있다. 따라서, 기존 연구들은 LoRA와 FT 간의 정확도 차이를 주로 학습 가능한 파라미터 수의 제한으로 설명하였으며, 다른 원인에 대한 추가 분석은 부족했다(Hu et al., 2022; Kopiczko et al., 2024).

Weight Normalization(Salimans & Kingma, 2016)에서 영감을 받아, 우리는 가중치 행렬을 크기(Magnitude)와 방향(Direction)으로 재매개변수화하여 최적화를 가속화하는 새로운 가중치 분해 분석(Weight Decomposition Analysis)을 도입한다. 우리의 분석은 가중치 행렬을 두 개의 독립된 구성 요소(크기와 방향)로 재구성하여 LoRA와 FT의 학습 패턴의 근본적인 차이를 밝혀낸다.

 

분석 방법

이 분석은 사전 학습된 가중치에 대한 LoRA와 FT의 크기 및 방향 업데이트를 조사하여 두 방법의 학습 행동의 근본적인 차이를 밝히고자 한다. 가중치 분해는 다음과 같이 공식화된다:

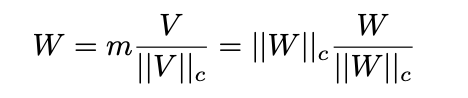
여기서 ∣∣W∣∣c는 각 열에 대한 벡터 정규화 값이고, W/∣∣W∣∣c는 단위 벡터를 나타낸다. 이 구성에서,

• m∈R1×k: 크기 벡터
• V∈Rd×k: 방향 행렬
  로 분해된다.

이 분해는 ∣∣V∣∣c의 각 열이 단위 벡터를 유지하도록 보장하며, m의 해당 스칼라가 각 벡터의 크기를 정의한다.

---

분석 결과

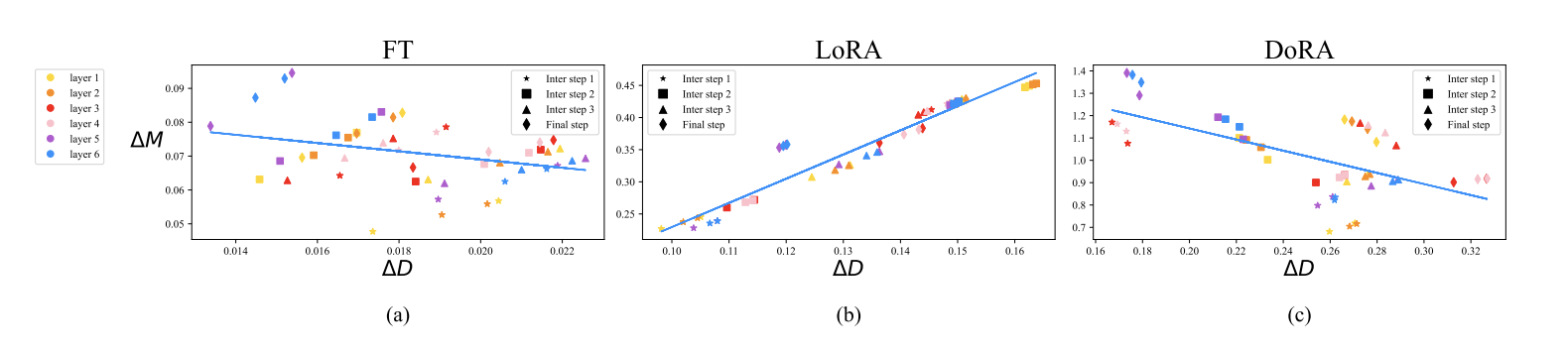
• Figure 2 (a)와 (b)는 FT와 LoRA의 쿼리 가중치 행렬 변화를 보여준다.
• LoRA는 훈련 단계 전반에서 방향과 크기 변화 간 비례 관계(양의 기울기)를 유지하며 일정한 학습 패턴을 보인다.
• FT는 더 다양한 학습 패턴을 보이며, 방향과 크기 변화 간의 관계가 비선형적이고 음의 기울기를 포함한다.

이 결과는 LoRA가 크기와 방향 업데이트를 동시에 학습하는 데 어려움을 겪으며, FT가 가진 섬세한 방향 조정을 수행하지 못한다는 것을 시사한다. LoRA의 이러한 제한은 학습 능력의 차이를 설명하며, 이를 개선하기 위해 FT와 더 유사한 학습 패턴을 가지는 LoRA 변형을 제안한다.

 

4. Method 해석

4.1. Weight-Decomposed Low-Rank Adaptation (DoRA)

DoRA는 가중치 분해 분석(Weight Decomposition Analysis)에서 얻은 통찰을 바탕으로 설계된 방법이다. DoRA의 핵심 아이디어는 다음과 같다:

1. 사전 학습된 가중치를 크기(Magnitude)와 방향(Direction)으로 분해한다.
2. 방향은 LoRA 방식으로 학습하고, 크기는 독립적으로 조정한다.

DoRA의 설계 원리

1. LoRA의 한계를 개선:
   기존 LoRA는 크기와 방향을 동시에 학습해야 했기 때문에 학습이 복잡해졌지만, DoRA는 방향 학습에 집중하면서도 크기는 따로 학습하도록 설계했다.
   → 학습이 더 간단해지고 효율적이다.
2. 학습 안정성 개선:
   가중치를 크기와 방향으로 분해하면, 방향 업데이트가 더 안정적으로 최적화된다. 이 부분은 Section 4.2에서 다룬다.

DoRA의 초기화

• DoRA는 사전 학습된 가중치 W0를 기준으로 시작한다: W0=m⋅V 여기서 m=∣∣W0∣∣c (크기), V (정규화된 방향)이다.
• 방향 V는 고정(frozen)된 상태로 유지되며, 크기 m은 학습 가능한 벡터로 설정된다.
• 방향 업데이트 ΔV는 LoRA 방식(저랭크 행렬 분해 B⋅A)으로 학습된다.

DoRA의 수식

최종 DoRA의 가중치는 다음과 같이 정의된다:

​

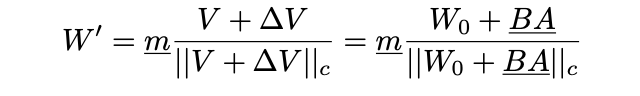
여기서 BA는 방향 업데이트를 나타내며, B와 A는 LoRA와 동일하게 초기화된다.

---

DoRA vs LoRA vs FT

• FT (Full Fine-Tuning):
  크기와 방향을 모두 섬세하게 학습하며, ΔM과 ΔD간 음의 상관관계를 가진다.
• LoRA:
  크기와 방향을 동시에 비례적으로 학습하며, ΔM과 ΔD간 양의 상관관계를 보인다.
• DoRA:
  FT와 유사하게 ΔM과 ΔD간 음의 상관관계를 가지며, FT의 학습 패턴을 더 잘 모방한다.

결론

DoRA는 FT와 유사한 학습 패턴을 가지면서도 LoRA의 효율성을 유지하며, 학습 능력과 안정성을 동시에 개선한다.

 

4.2. Gradient Analysis of DoRA

DoRA의 학습 패턴이 어떻게 안정적으로 이루어지는지 그래디언트 분석을 통해 설명한다.

1. DoRA의 그래디언트

• 핵심 특징:
  • ∇W′L(손실의 가중치 그래디언트)는 방향 벡터의 정규화에 의해 스케일 조정되며, 방향 벡터에서 멀어지는 형태로 투영된다.
  • 이로 인해 그래디언트의 공분산 행렬이 더 균등하게 정렬되므로, 최적화가 더 안정적이게 된다.

2. DoRA의 학습 패턴

두 가상의 업데이트 시나리오:

• S1: 작은 방향 변화 (ΔD)
• S2: 큰 방향 변화 (ΔD)

결과적으로:

• S1은 크기 변화가 크고 방향 변화가 작다.
• S2는 크기 변화가 작고 방향 변화가 크다.

이러한 관계를 통해 DoRA는 FT와 비슷한 학습 패턴을 보이며, LoRA보다 더 섬세한 업데이트가 가능해진다.

 

4.3. Training Overhead 감소

DoRA는 메모리 사용량을 줄이기 위해 다음과 같은 방법을 사용한다:

• 정규화 항 ∣∣V+ΔV∣∣c를 상수로 간주하여, 그래디언트 계산에서 제외한다.

이 방법으로 백워드 패스의 메모리 사용량을 크게 줄이면서도 정확도에는 거의 영향을 미치지 않는다.

• LLaMA 모델에서 메모리 사용량이 약 24.4% 감소
• VL-BART 모델에서는 약 12.4% 감소

 

5. Experiments (실험)

실험 목적

DoRA의 성능을 다양한 작업에서 검증한다:

1. 언어 작업: LLaMA 모델의 상식 추론 실험.
2. 멀티모달 작업: VL-BART 모델을 이용해 이미지/비디오-텍스트 이해 실험.
3. 시각적 지시 튜닝: LLaVA-1.5-7B 모델을 활용한 시각적 지시 작업.
4. Ablation Study: DoRA와 LoRA의 성능을 다양한 환경에서 비교하고, DoRA의 효율성과 세부 조정 능력을 분석.

---

5.1. Commonsense Reasoning (상식 추론)

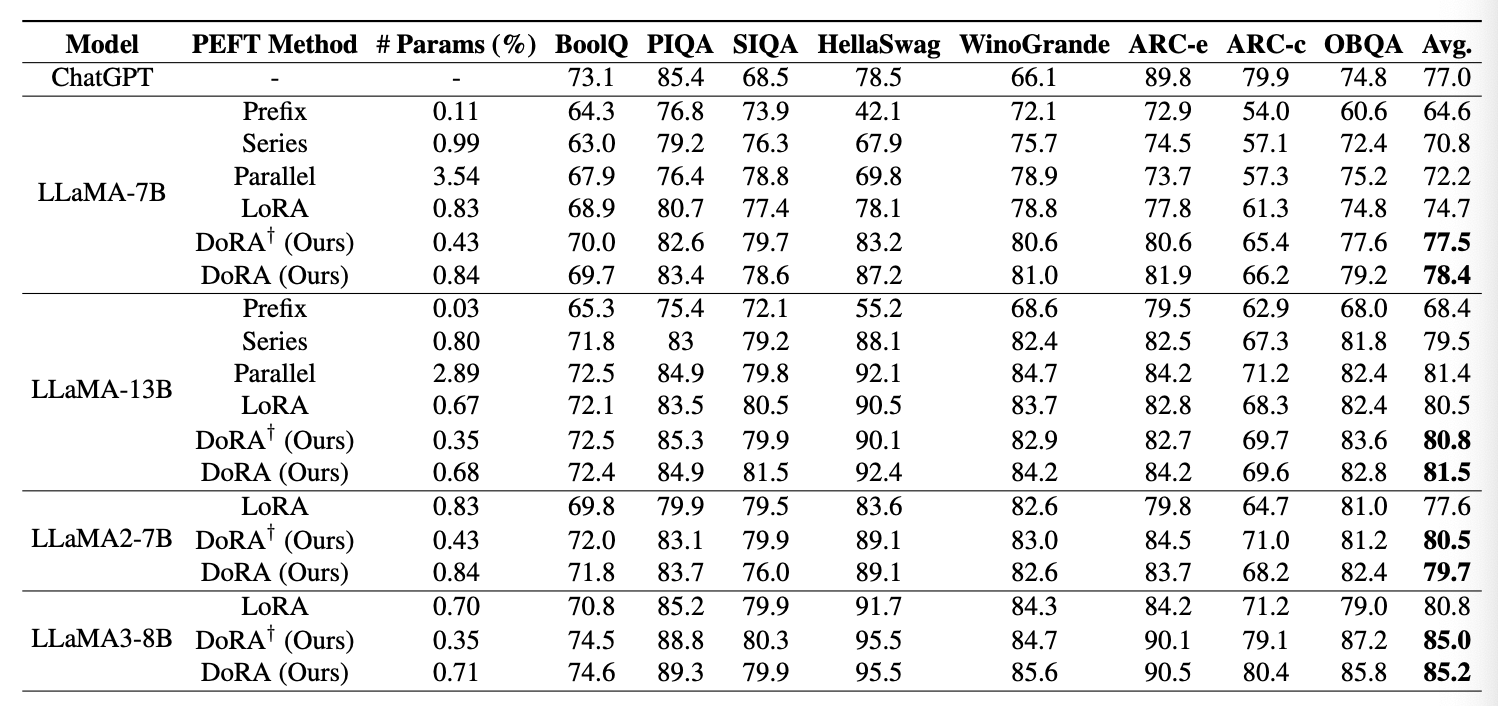
• 평가 모델: LLaMA-7B/13B, LLaMA2-7B, LLaMA3-8B
• 비교 대상: LoRA와 다른 PEFT 기법들 (Prompt Learning, Series Adapter, Parallel Adapter), 그리고 ChatGPT (GPT-3.5-turbo API)
• 설정:
  • 8개의 상식 추론 하위 작업의 학습 데이터를 합쳐서 학습하고 개별 테스트셋에서 평가.
  • DoRA는 LoRA의 설정을 따르며, 학습률만 조정.
  • DoRA는 학습 가능한 크기 파라미터가 추가되지만, 이는 0.01% 정도만 증가한다.

결과

1. DoRA vs LoRA
   • LLaMA-7B: LoRA보다 3.7% 정확도 향상.
   • LLaMA-13B: LoRA보다 1% 높으며, Parallel Adapter와 비슷한 정확도.
   • LLaMA2-7B와 LLaMA3-8B: LoRA 대비 각각 2.1%, 4.4% 성능 향상.
2. DoRA† (랭크를 LoRA의 절반으로 줄인 버전)
   • LLaMA-7B: LoRA보다 2.8% 성능 향상.
   • LLaMA2-7B와 LLaMA3-8B에서도 여전히 성능 우위를 보임.

분석

• DoRA는 사전 학습된 가중치의 크기와 방향을 더 미세하게 조정하기 때문에 성능이 높아진다.
• 가설 검증: DoRA는 크기와 방향의 변화량이 LoRA에 비해 작아도 더 효과적으로 적응한다. 이는 Figure 3에서 확인된다.

---

5.2. Multi-Task Image/Video-Text Understanding (멀티태스크 이미지/비디오-텍스트 이해)

• 평가 모델: VL-BART
• 작업:
  • 이미지-텍스트: VQAv2, GQA, NLVR2, MSCOCO
  • 비디오-텍스트: TVQA, How2QA, TVC, YC2C
• 설정: LoRA와 동일한 하이퍼파라미터 및 설정 사용.

결과

1. 이미지-텍스트 작업
   • DoRA는 LoRA보다 1% 높은 정확도를 달성하며, FT의 성능에 도달함.
2. 비디오-텍스트 작업
   • DoRA는 LoRA보다 2% 높은 정확도를 기록.

---

5.3. Visual Instruction Tuning (시각적 지시 튜닝)

• 평가 모델: LLaVA-1.5-7B (Vicuna-1.5-7B와 CLIP ViT-L/336px로 구성된 모델)
• 데이터셋: VQA, OCR, 지역 수준 VQA, 시각적 대화 데이터, 언어 대화 데이터
• 설정: LoRA와 동일한 설정 사용.

결과

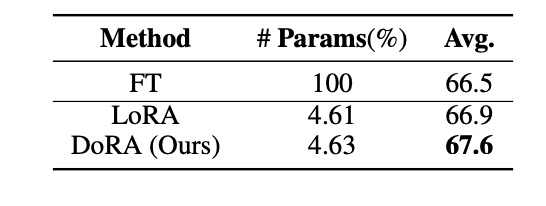
1. LoRA vs FT
   • LoRA의 평균 정확도가 FT보다 높은 경우가 발생. 이는 FT가 오버피팅 문제를 겪을 가능성을 시사한다.
2. DoRA 성능
   • LoRA 대비 평균 0.7% 정확도 향상.
   • FT 대비 평균 1.1% 정확도 향상.

5.4. Compatibility of DoRA with Other LoRA Variants (DoRA와 다른 LoRA 변형의 호환성)

목적

• DoRA가 다른 LoRA 변형과 호환되는지를 검증하기 위해 VeRA(Kopiczko et al., 2024)를 사례로 선택한다.
• VeRA는 모든 레이어에서 고유한 저랭크 행렬 쌍을 공유하고, 레이어별 학습 가능한 스케일링 벡터만 추가하는 방법으로 파라미터를 크게 줄인다.

실험 설계

• VeRA를 DoRA의 방향 업데이트(ΔV)에 적용하여 DVoRA를 구성한다.
• LLaMA-7B와 LLaMA2-7B 모델을 Alpaca 데이터셋의 10K 서브셋으로 Instruction Tuning 수행.
• 평가: MT-Bench 벤치마크(80개의 멀티턴 질문)를 GPT-4를 통해 점수화(10점 만점). 

결과

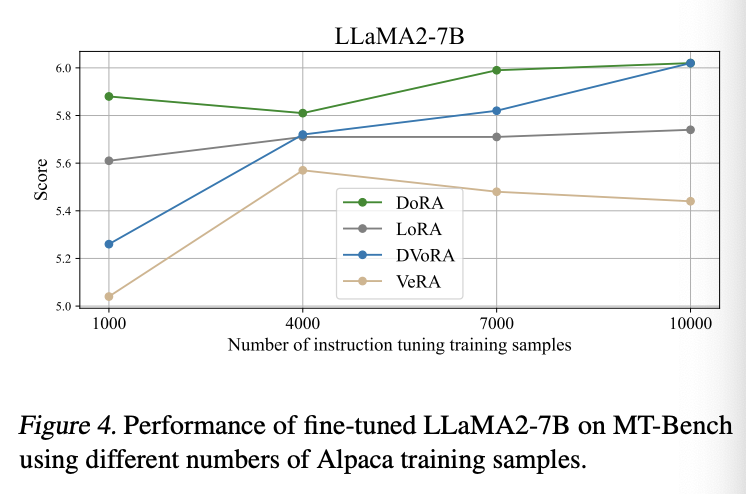
• DVoRA와 DoRA는 VeRA와 LoRA를 일관되게 능가한다.
  • DVoRA: VeRA 대비 LLaMA-7B에서 0.7점, LLaMA2-7B에서 0.5점 더 높은 성능을 보인다.
  • DVoRA는 VeRA의 파라미터 효율성을 유지하면서도 LoRA 수준의 성능을 달성한다.
• 다양한 훈련 샘플 수(1000, 4000, 7000, 10000)에서 비교했을 때, DoRA와 DVoRA는 LoRA와 VeRA를 꾸준히 능가한다.
  • 예시: 7000개 샘플에서 DoRA와 DVoRA는 LoRA와 VeRA보다 각각 0.3점과 0.33점 높음.
  • 1000개 샘플에서도 성능 우위를 유지(DoRA: 0.29점, DVoRA: 0.22점 리드).

---

5.5. Robustness of DoRA towards Different Rank Settings (랭크 설정에 따른 DoRA의 강건성)

목적

• LoRA와 DoRA의 성능을 다양한 랭크 값(r∈{4,8,16,32,64})에 대해 비교한다.

결과

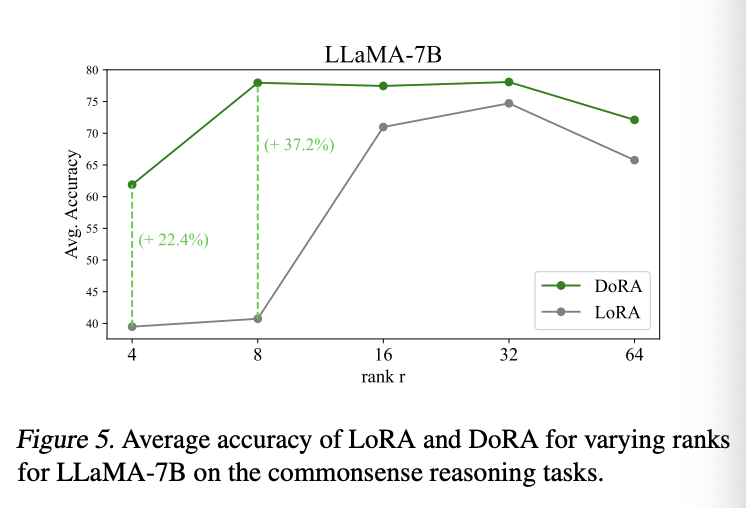
• DoRA는 모든 랭크 설정에서 LoRA를 일관되게 능가한다.
  • 특히, 낮은 랭크(r=4, 8)에서 LoRA의 성능이 급격히 하락하지만, DoRA는 성능을 더 잘 유지한다.
    • LoRA: r=8에서 40.74%, r=4에서 39.49%
    • DoRA: r=8에서 77.96%, r=4에서 61.89%
• 결론: DoRA는 낮은 랭크 설정에서도 강건한 성능을 보이며, LoRA보다 훨씬 더 안정적이다.

---

5.6. Tuning Granularity Analysis (튜닝 세분화 분석)

목적

• 크기와 방향 업데이트 중 어떤 부분이 더 중요하며, 학습 가능한 파라미터를 더 줄일 수 있는지 검토한다.

설정

• LoRA: 모든 Multi-Head Attention(MHA) 및 MLP 레이어를 업데이트해야 최적의 성능 달성.
• DoRA:
  • QKV 모듈에서는 방향과 크기 모두를 업데이트.
  • 나머지 MLP 레이어는 크기만 업데이트.

결과

• DoRA는 학습 가능한 파라미터 수를 절반 이하로 줄이면서도 LoRA를 능가한다.
  • LLaMA-7B: LoRA보다 2.8% 정확도 향상.
  • LLaMA-13B: LoRA보다 0.8% 정확도 향상.

 

6. Broader Impacts (광범위한 영향)

6.1. QDoRA: QLoRA에 대한 개선

• 배경: QLoRA(Dettmers et al., 2023)는 사전 학습된 모델을 4비트 양자화하고 LoRA를 그 위에 적용하여 GPU 메모리 사용량을 크게 줄이는 방법이다. 하지만 여전히 초기 모델 로딩 시 많은 메모리가 필요하다.
• QDoRA: 최근 연구(Kerem Turgutlu, 2024)에서는 QLoRA에서 LoRA 대신 DoRA를 사용한 QDoRA를 제안했다. 이 과정에서 Fully Sharded Data Parallel (FSDP) 방식을 적용해 모델을 여러 GPU에 분할하고 병렬 학습을 가능하게 했다.

실험 설정

• 모델: LLaMA2-7B와 LLaMA3-8B
• 데이터셋: Orca-Math (100K 학습 샘플, 500개 평가 샘플)
• 평가 지표: 정확 일치 점수 (Exact Match Score)
• 비교 방법: QLoRA, QDoRA, FT(Full Fine-Tuning), FT 후 양자화(PTQ)

결과

• QDoRA는 QLoRA보다 높은 성능을 보이며, FT도 약간 능가한다:
  • LLaMA2-7B: QLoRA 대비 0.19점 향상.
  • LLaMA3-8B: QLoRA 대비 0.23점 향상.
• 의미: QDoRA는 QLoRA의 파라미터 효율성과 FT의 세밀한 최적화를 결합하면서도 메모리 사용량은 현저히 적다.
• 기대 효과: QDoRA는 GPU 메모리 요구를 크게 낮춰, 오픈소스 커뮤니티에 큰 혜택을 제공할 수 있다.

 

6.2. Text-to-Image Generation (텍스트-이미지 생성)

• 배경: 확산 모델(Diffusion Models)이 대형화됨에 따라, LoRA는 Stable Diffusion 모델 미세조정에 자주 사용된다.
• 목적: DoRA의 이점이 텍스트-이미지 생성 작업에서도 LoRA를 능가하는지 확인한다.
• 실험 설정:
  • 모델: SDXL (Podell et al., 2023)
  • 학습 방식: DreamBooth(Ruiz et al., 2023)의 학습 파이프라인 사용.
  • 데이터셋: 3D 아이콘 및 레고 세트
  • 조건: LoRA와 DoRA의 하이퍼파라미터는 동일하게 설정하며, 동일한 시드(seed)를 사용해 이미지를 생성.

결과

• DoRA는 LoRA보다 더 나은 개인화 성능을 보이며, 학습 목표를 더 정확하게 반영한다.
  • 예: 3D 아이콘 이미지에서 DoRA 출력물은 이미지 주변의 둥근 사각형을 정확히 재현한 반면, LoRA는 이 특징을 재현하지 못했다.
  • 레고 데이터셋에서도 DoRA는 생성된 이미지에 레고 로고를 일관되게 포함시켰지만, LoRA는 이를 구현하지 못했다.

 

7. Conclusion (결론)

• 이 연구에서는 가중치 분해 분석을 통해 LoRA와 FT의 학습 패턴 차이를 규명했다.
• 이를 기반으로 DoRA를 제안했으며, DoRA는 다음과 같은 특징을 가진다:
  1. FT의 학습 패턴과 더 유사하면서도, LoRA와 호환되는 미세조정 방법.
  2. 다양한 작업과 모델 아키텍처에서 LoRA를 일관되게 능가한다.
     • 상식 추론, 시각적 지시 튜닝 등에서 성능 향상.
  3. VeRA와의 호환성 검증을 통해 확장성을 입증했다.
  4. 학습 후 추론 시 추가 비용 없이 크기와 방향을 병합할 수 있어 효율적이다.
• 미래 연구 방향: 언어 및 비전 도메인 외에도 오디오 분야 등으로 DoRA의 일반화 가능성을 탐구할 예정이다.

 

 

 

---

내가 궁금했던 것들

1. 왜 방향 중심 학습인데도 크기를 학습하는가?

LoRA와 DoRA의 차이를 이해하기 위해 먼저 방향과 크기의 역할을 이해해야 해.

• 방향(Direction):
  가중치 벡터가 향하는 방향. 이는 학습 데이터의 특성과 연관되며, 모델이 학습하는 주요 "패턴"이나 "정보"를 담는다.
  → 학습의 핵심적인 부분이며, 모델의 성능에 큰 영향을 미친다.
• 크기(Magnitude):
  방향 벡터의 길이(스칼라). 크기는 "얼마나 강하게 업데이트할지"를 결정하는 역할을 한다.
  → 방향에 담긴 정보를 어느 정도로 강조하거나 약화할지를 조정하는 보조적인 역할이다.

DoRA에서 크기를 학습하는 이유: 방향과 크기는 서로 독립적이다.

• 방향만 학습하고 크기를 고정하면, 특정 상황에서는 업데이트가 비효율적일 수 있다.
• 예를 들어, "방향은 맞지만, 크기를 조정해서 더 강조해야 하는 경우"가 발생한다.

1. 섬세한 업데이트를 위해 크기와 방향을 동시에 조정해야 한다.
   • LoRA에서는 크기와 방향이 섞여 있으므로 둘을 동시에 제어하기 어렵다.
   • DoRA는 크기와 방향을 분리하여 학습하므로, 방향을 유지하면서 크기만 조정하거나, 크기를 유지하면서 방향만 조정하는 미세 조정이 가능하다.

---

2. 크기를 학습하는 방식 vs. 방향을 학습하는 방식의 차이

크기를 학습하는 방식 (Magnitude)

• 크기는 단순한 스칼라 값으로, 각 벡터의 길이를 나타낸다.
• 학습 방식: 크기 값(∣∣W∣∣c||W||_c∣∣W∣∣c​)은 독립적으로 학습되며, 방향 정보와 분리되어 있다.
• 역할: "업데이트의 강도"를 조정하며, 방향에 담긴 정보를 얼마나 강조할지 결정한다.
• 특징: 상대적으로 계산이 간단하며, 크기 조정만 필요할 경우에는 방향을 건드리지 않는다.

방향을 학습하는 방식 (Direction)

• 방향은 정규화된 벡터로, 학습 데이터에서 패턴을 나타낸다.
• 학습 방식: LoRA의 방식(저랭크 행렬 분해)을 활용해 효율적으로 학습한다.
  • 방향 업데이트는 두 저랭크 행렬 BBB와 AAA를 곱하여 표현된다.
  • ΔW=B⋅A\Delta W = B \cdot AΔW=B⋅A: 이 업데이트는 방향 조정만 수행한다.
• 특징: 방향 학습은 데이터의 본질적인 구조를 학습하므로, 더 많은 계산 자원이 필요할 수 있다.
  그러나 LoRA 방식 덕분에 계산량이 줄어든다.

---

3. 크기와 방향을 따로 학습하면 자원이 더 드는 것 아닌가?

자원 사용 증가

• 크기와 방향을 따로 학습하면 이론적으로 자원이 더 들 수 있다.
  → 크기 학습과 방향 학습을 동시에 수행해야 하기 때문.

효율성 확보

DoRA는 자원 사용을 최소화하기 위해 다음과 같은 방법을 사용한다:

1. 방향 학습에 LoRA 방식 사용:
   LoRA는 방향 학습에서 저랭크 행렬 분해를 사용하므로, 계산량을 기존 FT보다 훨씬 줄인다.
2. 크기 학습은 간단한 스칼라 조정:
   크기는 단순히 벡터의 길이를 조정하는 작업이므로, 계산량이 작다.

결론적으로, 크기와 방향을 분리하면 학습 패턴의 유연성이 높아지며, 이로 인해 더 좋은 성능을 낼 수 있다. 자원 사용은 약간 증가할 수 있지만, LoRA 방식의 효율성을 활용하면 실질적인 부담은 크지 않다.

---

4. 왜 DoRA가 LoRA보다 섬세한 학습이 가능한가?

LoRA는 크기와 방향을 한꺼번에 업데이트하므로 다음과 같은 한계가 있다:

• "크기만 조정해야 하는 상황"에서 방향까지 같이 바뀌어 버릴 수 있다.
• 반대로, "방향만 섬세하게 바꿔야 하는 상황"에서 크기도 같이 조정되어 버린다.

DoRA는 크기와 방향을 분리하여 각각 학습하므로:

1. 방향을 유지하면서 크기만 조정하거나,
2. 크기를 유지하면서 방향만 조정할 수 있다.

이로 인해 더 섬세하고 유연한 학습이 가능해지고, FT와 유사한 학습 패턴을 구현할 수 있다.