이전 포스팅 3-1에서는 Model-Free Prediction을 공부했다. 지금부터는 Control에 대해 배워볼 것 이다.
우선 차이를 다시 되짚고 넘어가자.
Prediction과 Control의 과정:
- Prediction (정책 평가, Policy Evaluation):
- 주어진 정책 π를 따를 때 각 상태의 가치 함수 Vπ(s)를 추정하는 과정이다.
- 이 단계에서는 정책이 고정되어 있고, 정책을 따를 때 상태가 얼마나 좋은지를 예측한다.
- Value Function Vπ(s): 현재 정책에 따라 상태에서 기대되는 미래 보상의 합을 의미한다.
- Control (정책 개선, Policy Improvement):
- Prediction 결과로 나온 상태 가치 함수 Vπ(s)를 바탕으로, 각 상태에서 더 나은 행동을 선택하여 정책을 개선하는 과정이다.
- 이 단계에서는 각 상태에서 가장 좋은 행동을 선택하여 새로운 정책을 만든다.
- 정책이 개선된 후, 그 정책에 따른 상태 가치를 다시 평가하는 과정으로 돌아가면서 최적 정책을 찾아간다.

On-policy learning은 자신이 직접 시행착오를 격으면서 스스로 배우는 것에 비유를 할 수 있다. 동일한 policy인 파이에 대하여 샘플링된 경험을 따르면서 이를 통해서 학습을 하는 방식을 의미한다.
Off-policy learning은 다른이가 시행착오를 겪는것을 보면서 배우는 것에 비유를 할 수 있다. 다른 policy인 뮤에 대해서 샘플링된 경험을 따르면서 자신의 policy 파이를 학습하는 방식을 의미한다.
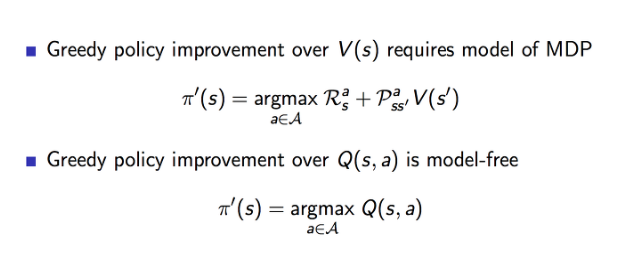
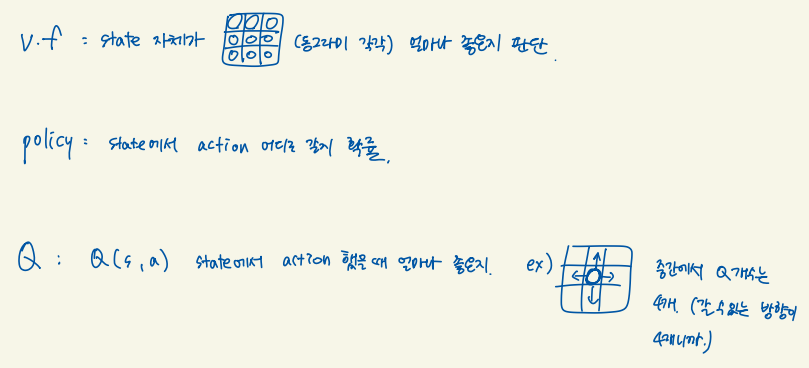
상단에 V(s)는 state에 대한 value function을 추정해야하기 때문에 MDP 모델을 사용하는 형태이다.
하단에 Q(s,a)는 s state에 대하여 a action을 취했을때 가장 큰 Q 값을 갖는 best action을 사용하게 되므로 model-free에 해당하는 방식이다.
V 대신에 Q 를 사용해서 state-action value 를 업데이트 하도록 하여 policy evaluation과 improvement를 반복한다. 최적의 q*를 찾게 되면 최적의 policy를 찾을 수 있다.

- 탐험과 활용의 균형:
- 확률 1−ϵ1 - \epsilon로 현재 가장 좋은 행동(greedy action)을 선택한다. 즉, 현재 가치 함수에서 가장 높은 보상을 줄 것으로 예상되는 행동을 선택한다.
- 확률 ϵ로 무작위로 행동을 선택한다. 이때 모든 행동은 작은 확률로라도 선택될 가능성이 있다.
- ϵ 확률로 무작위 행동을 선택하므로, 모든 행동이 비록 낮은 확률이라도 시도될 가능성이 있다. 이는 새로운 행동을 탐험하는 것을 보장해준다.
- 탐험과 활용을 조정하는 방법으로, 대부분은 가장 좋은 행동을 선택하지만, 가끔은 무작위로 행동하여 새로운 것을 탐험한다.
- ϵ이 클수록 더 많은 탐험이 이루어지고, 작을수록 더 많이 현재 좋은 행동을 선택하게 된다.
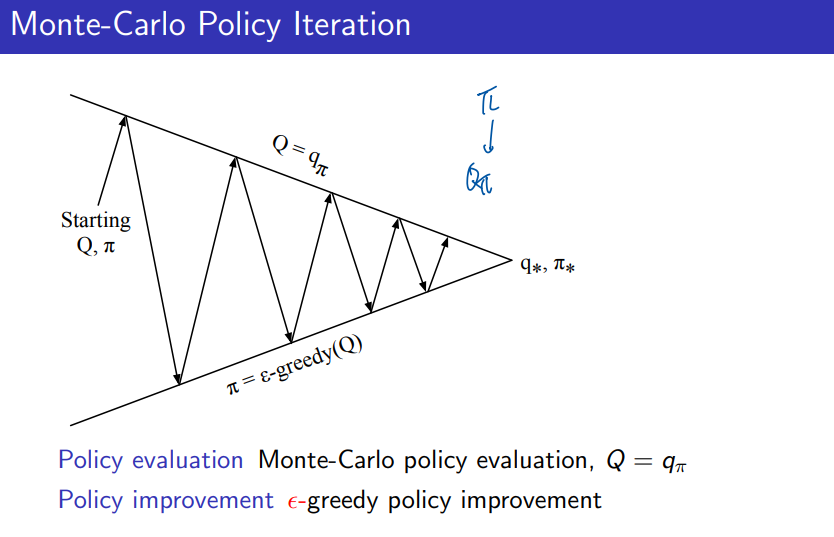
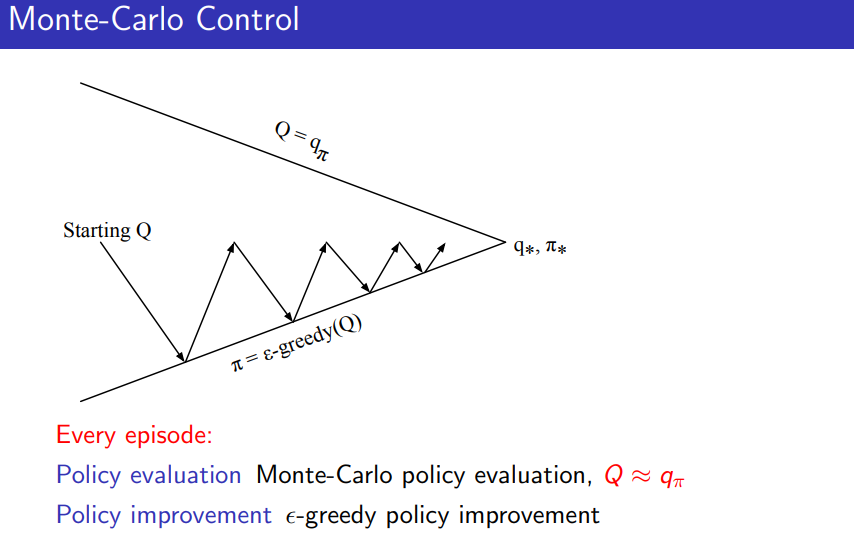
- Monte Carlo Policy Iteration은 정책 평가와 정책 개선을 교대로 수행하면서 점진적으로 최적 정책에 수렴한다.
- Monte Carlo Control은 매 에피소드마다 정책 평가와 정책 개선이 동시에 이루어지며, 더 빠르게 최적 정책으로 수렴하는 경향이 있다.

- Prediction = Policy Evaluation:
- Prediction은 주어진 정책이 얼마나 좋은지를 평가하는 과정으로, 이는 Policy Evaluation이다. 즉, 현재 정책을 따를 때 각 상태의 가치를 계산하는 과정이다.
- Control = Policy Improvement + Policy Evaluation:
- Control은 정책을 개선하는 과정인데, 이때 항상 정책 평가와 정책 개선이 교대로 일어난다.
- Policy Evaluation (eval): 현재 정책이 얼마나 좋은지를 평가하는 과정 (즉, 상태 가치를 구하는 과정).
- Policy Improvement (imp): 평가된 결과를 바탕으로, 더 나은 행동을 선택하여 정책을 개선하는 과정.

GLIE는 Greedy in the Limit with Infinite Exploration의 약자로, 무한 탐험을 하면서도 최종적으로는 탐욕적(Greedy) 정책에 수렴하는 것을 의미한다. 이는 강화학습에서 탐험과 활용을 균형 있게 처리하는 중요한 개념이다.

ε-Greedy와 GLIE:
- ε-Greedy 정책은 GLIE 조건을 만족할 수 있다. 탐험을 지속하면서도 시간이 지나면 점차 탐욕적 정책으로 수렴하게 된다.
- 예를 들어, ε-Greedy 방법에서 ε이 점차 줄어드는 경우, 초기에는 탐험을 많이 하지만, 시간이 지남에 따라 탐험을 줄이고 탐욕적인 행동을 점점 더 많이 선택하게 된다.
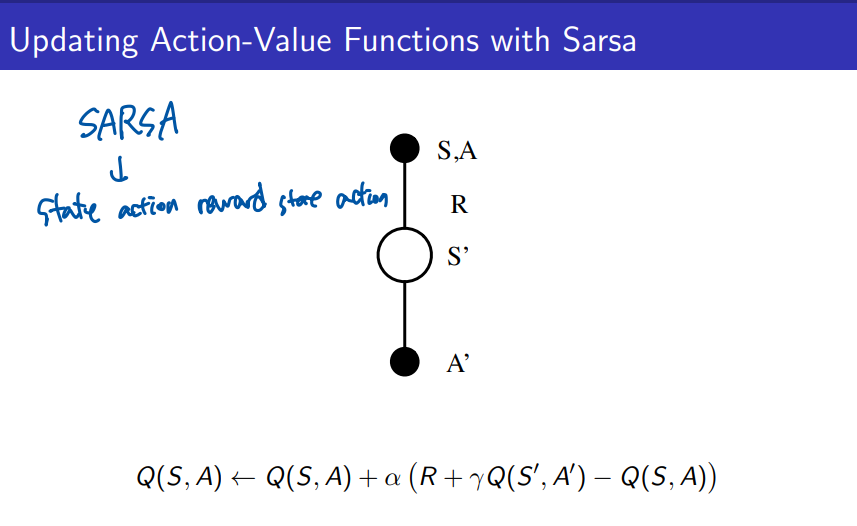
SARSA 알고리즘이란?
- SARSA는 State-Action-Reward-State-Action의 약자로, 각 단계에서 상태, 행동, 보상, 다음 상태, 다음 행동을 기반으로 학습하는 알고리즘이다. 이 알고리즘은 on-policy 강화학습 방법으로, 현재의 정책에 따라 행동을 선택하고 그에 따른 Q-함수를 업데이트한다.
SARSA의 작동 원리:
- S, A: 에이전트가 현재 상태 에서 행동 A를 선택한다.
- R: 그 행동을 수행한 후 보상 R을 얻는다.
- S': 에이전트는 다음 상태 S′로 전이한다.
- A': 다음 상태 S′에서 새로운 행동 A′를 선택한다.
SARSA는 이 일련의 과정(S -> A -> R -> S' -> A')을 사용해 Q-함수를 업데이트한다.
Q-함수 업데이트 식:
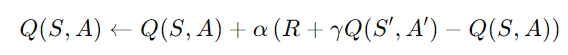


1. n-Step SARSA:
- n-Step SARSA는 몇 단계(n-step) 후의 보상을 얼마나 고려할지 결정하는 방법이다.
- n=1일 때는 일반적인 SARSA (한 단계만 고려).
- n=∞일 때는 Monte Carlo 방식으로, 전체 에피소드를 고려한다.
- 중간 단계인 n=2, 3, ...에선 해당 단계만큼 보상을 계산해 업데이트.

2. Forward View SARSA(λ):
- λ-SARSA는 여러 n-step SARSA 결과들을 가중 평균해서 업데이트한다.
- λ는 여러 단계(n-step) 사이의 가중치를 조절해주며, 이를 통해 TD(1)부터 Monte Carlo(∞)까지 다양하게 조정할 수 있다.
- 이 방식은 n-step이 아닌 모든 단계를 적절히 반영한 Q값을 계산하는 방식이다.
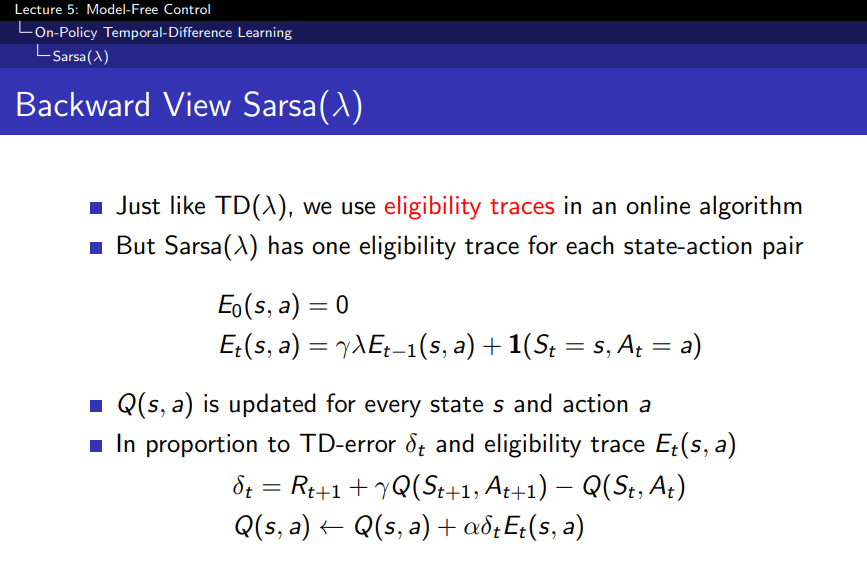
3. Backward View SARSA(λ):
- Eligibility Traces(자격 추적)를 사용해 이전 상태-행동 쌍에 대한 영향력을 추적하면서 업데이트한다.
- Forward View가 이론적인 설명이라면, Backward View는 실질적으로 구현 가능한 방식이다.
- δt라는 TD 오류값과 자격 추적을 이용해 과거에 있던 상태-행동 쌍의 가치를 업데이트한다.
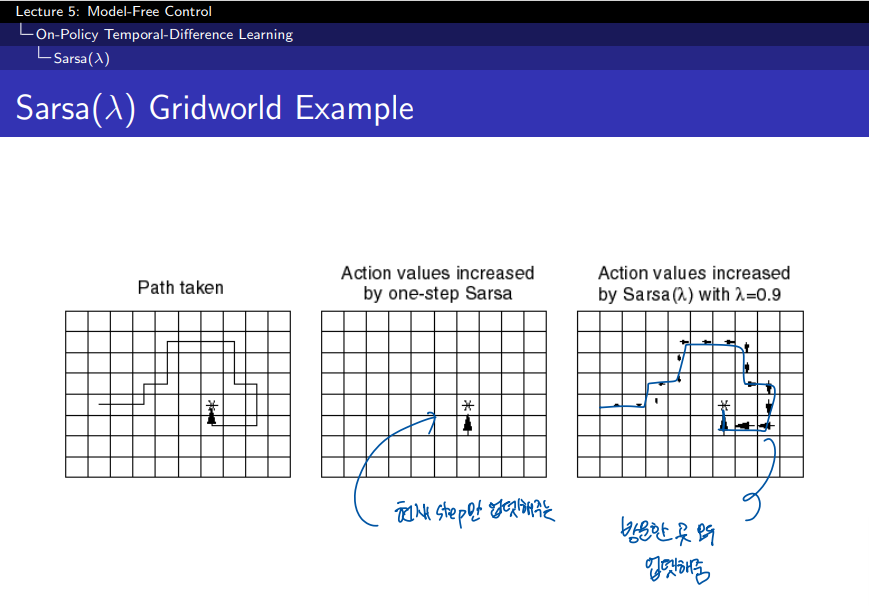
왼쪽 그림 (Path taken):
- 에이전트가 움직인 경로를 나타낸다. 에이전트는 시작점에서 목표 지점(별 표시)까지 특정 경로를 따라 이동했다.
가운데 그림 (One-step SARSA):
- 한 단계 SARSA를 사용한 경우이다.
- 여기서 보이는 것은, 에이전트가 이동한 경로의 가치가 한 스텝만 반영된 상태이다. 즉, SARSA는 한 스텝 이후의 보상만을 반영하여 상태-행동 가치 함수를 업데이트했다.
- 에이전트가 지나간 경로에만 가치가 크게 증가했고, 이외의 경로는 거의 반영되지 않았다.
오른쪽 그림 (SARSA(λ)):
- λ 값을 사용한 SARSA(λ)로 학습한 경우이다. 여기서 λ = 0.9로 설정되었다.
- 이 경우는 에이전트가 지나간 경로 뿐만 아니라 다른 경로도 일부 반영된다. λ 값을 사용하면 여러 스텝에 걸친 보상을 더 많이 반영할 수 있기 때문이다.
- 이는 과거의 상태-행동 쌍들이 여러 스텝에 걸쳐 업데이트되어, 목표 지점에 가까워질수록 가치가 더 많이 증가하게 된다.


Q-Learning


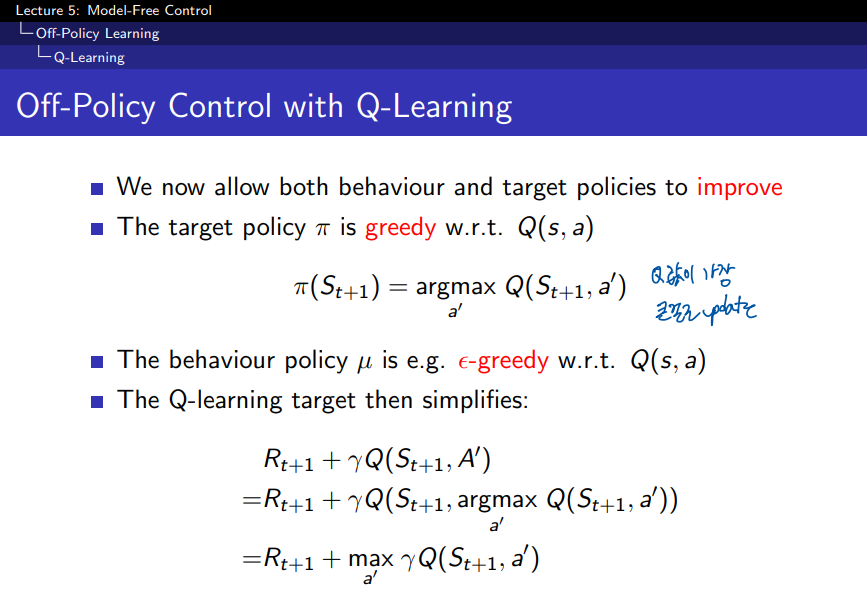



SARSA vs. Q-Learning:
1. SARSA (State-Action-Reward-State-Action):
- On-policy 방법: SARSA는 현재 에이전트가 실제로 선택한 행동에 기반해 Q-값을 업데이트한다.
- 즉, 다음 상태에서 실제로 선택한 행동 A′A'에 대한 Q-값을 사용한다.
- 업데이트 식:
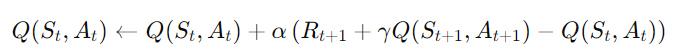
2. Q-Learning:
- Off-policy 방법: Q-Learning은 에이전트가 다음 상태에서 **가장 좋은 행동(탐욕적 행동)**을 취한다고 가정하고 Q-값을 업데이트한다.
- 즉, 실제로 선택한 행동과 상관없이, 다음 상태에서 최적의 행동을 가정하여 학습한다. 그래서 SARSA와는 달리, Q-Learning은 최적 정책을 따르는 학습 방식이라고 할 수 있다.
- 업데이트 식:
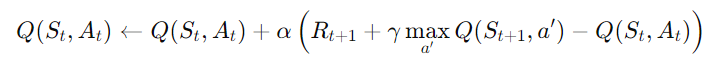
핵심 차이점:
- SARSA: 현재 정책에 따라 실제로 취한 행동을 기준으로 업데이트한다. 즉, 탐험적 행동도 반영되기 때문에 정책을 따르면서 학습하는 on-policy 방식이다.
- 따라서, 탐험적인 행동을 할 때 Q-값이 더 낮을 수 있다.
- Q-Learning: 다음 상태에서 최적의 행동을 취한다고 가정하고 업데이트한다. 탐욕적 행동을 기준으로 학습하므로 정책과 상관없이 더 나은 행동을 예측하는 off-policy 방식이다.
- 항상 최적의 Q-값을 추구하기 때문에 더 빠르게 수렴할 수 있다.
이 두 알고리즘의 차이는 실제로 선택한 행동을 기준으로 할 것인지, 최적의 행동을 기준으로 할 것인지에서 나타나는 것이다.
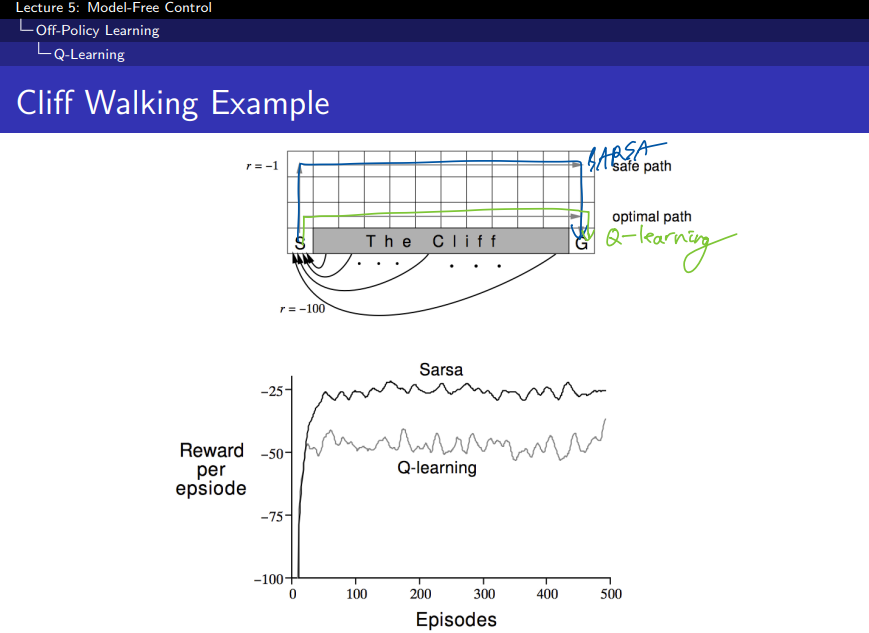
Cliff Walking 문제
- 목표: 에이전트는 출발점 S에서 시작하여 목적지 G에 도달해야 한다.
- 위험 요소: 에이전트가 절벽(Cliff)에 떨어지면 −100의 큰 보상을 받는다. 즉, 절벽은 피해야 한다.
- 일반적인 보상: 이동할 때마다 −1의 보상을 받는다. 즉, 최적 경로는 빠르게 목표에 도달하면서 절벽을 피하는 것이다.
SARSA와 Q-Learning의 경로 차이:
- SARSA:
- 안전한 경로를 택한다. SARSA는 on-policy 학습이기 때문에, 에이전트가 실제로 선택한 경로에 대해 학습한다.
- SARSA는 탐험적 행동을 고려하며, 절벽 근처에서 위험한 경로를 피하는 방향으로 학습되기 때문에, 비교적 안전한 경로를 택하게 된다.
- Q-Learning:
- 최적 경로를 찾는다. Q-Learning은 off-policy 학습이므로, 에이전트는 다음 상태에서 항상 최적의 행동을 한다고 가정하고 학습한다.
- Q-Learning은 보상을 극대화하기 위해 절벽 바로 옆을 지나가는 최단 경로를 찾는다. 이 경로는 빠르지만, 탐험 중에는 절벽에 떨어질 위험이 있다.
그래프 해석:
- X축: 에피소드 수 (학습이 진행될수록 에이전트는 더 많은 경험을 쌓는다).
- Y축: 에피소드 당 보상 (값이 높을수록 더 나은 성과).
- SARSA: 에피소드가 진행될수록 안정적으로 보상을 얻는다. 초기에는 탐험 중에 절벽에 떨어질 수도 있지만, 시간이 지나면 안전한 경로를 학습하게 된다.
- Q-Learning: Q-Learning은 최적의 경로를 찾는 동안 더 많이 절벽에 떨어지므로 보상이 더 낮게 시작된다. 하지만 시간이 지남에 따라 최적 경로를 학습하면서도 일부 절벽에 떨어지는 경우가 존재해 변동이 크다.
Relationship Between DP and TD
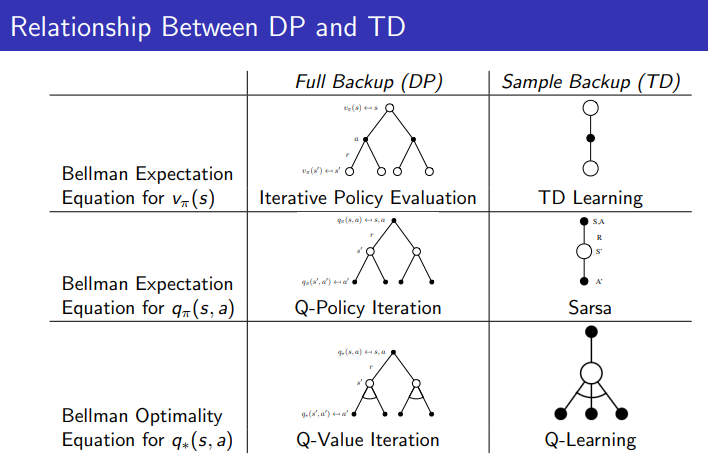
1.1 Full Backup (DP) vs Sample Backup (TD):
- Full Backup (DP): 동적 프로그래밍은 모델 기반으로 모든 상태에 대해 전이 확률을 사용하여 계산한다. 즉, 모든 가능한 다음 상태를 고려해 벨만 방정식을 사용해 값을 업데이트한다.
- Sample Backup (TD): 템포럴 디퍼런스는 모델 프리 방식으로 경험에서 샘플링된 데이터를 사용해 값을 업데이트한다. TD 학습은 한 번에 하나의 상태 전이를 고려해 업데이트한다.
1.2 각 학습 방식에 해당하는 알고리즘:
- Value Function:
- DP에서는 Iterative Policy Evaluation으로 상태 가치 V(s)를 평가한다.
- TD 학습에서는 경험을 바탕으로 TD Learning을 사용해 V(s)를 업데이트한다.
- Q-Function:
- DP에서는 Q-Policy Iteration을 통해 정책을 기반으로 상태-행동 가치 Q(s,a)를 평가한다.
- TD 학습에서는 SARSA를 사용해 현재 정책을 따르는 상태-행동 가치 Q(s,a)를 업데이트한다.
- Optimal Q-Function:
- DP에서는 Q-Value Iteration을 통해 최적의 상태-행동 가치 함수 Q∗(s,a)를 계산한다.
- TD 학습에서는 Q-Learning을 통해 최적의 상태-행동 가치 함수 Q∗(s,a)를 학습한다.
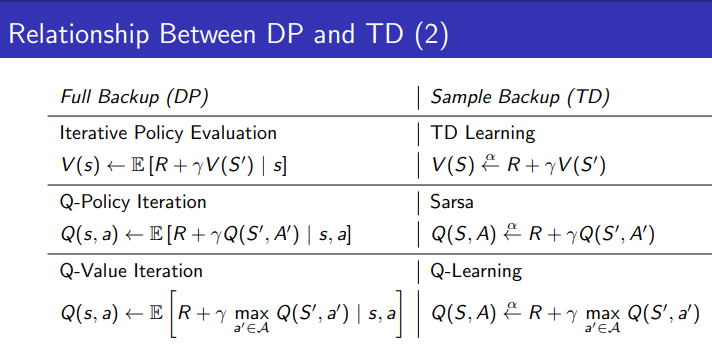
2.1 Value Function 업데이트 방식:
- DP (Full Backup): 벨만 기대 방정식을 사용하여 다음 상태의 모든 전이 확률을 고려해 값을 계산한다.
- TD (Sample Backup): 하나의 샘플 데이터를 기반으로 업데이트를 한다.
2.2 Q-Function 업데이트 방식:
- DP (Full Backup): 모든 가능한 다음 상태와 행동에 대해 기대값을 계산한다.
- TD (Sample Backup): SARSA를 통해 실제 행동과 결과에 따라 Q-값을 업데이트한다.
2.3 Optimal Q-Function 업데이트 방식:
- DP (Full Backup): 최적 행동을 고려해 모든 상태 전이에 대해 업데이트한다.
- TD (Sample Backup): Q-Learning을 통해 샘플된 경험에서 최적의 행동을 찾아 업데이트한다.
'AI > RL' 카테고리의 다른 글
| [RL] 4-1 Value Function Approximation (0) | 2024.10.13 |
|---|---|
| [RL] 3-1 Model-Free Prediction - (TD lambda) (2) | 2024.10.12 |
| [RL] 3-1 Model-Free Prediction - (TD) (0) | 2024.10.09 |
| [RL] 3-1 Model-Free Prediction - (MC) (0) | 2024.10.09 |
| [RL] 2-2 Planning by Dynamic Programming (0) | 2024.10.09 |
이전 포스팅 3-1에서는 Model-Free Prediction을 공부했다. 지금부터는 Control에 대해 배워볼 것 이다.
우선 차이를 다시 되짚고 넘어가자.
Prediction과 Control의 과정:
- Prediction (정책 평가, Policy Evaluation):
- 주어진 정책 π를 따를 때 각 상태의 가치 함수 Vπ(s)를 추정하는 과정이다.
- 이 단계에서는 정책이 고정되어 있고, 정책을 따를 때 상태가 얼마나 좋은지를 예측한다.
- Value Function Vπ(s): 현재 정책에 따라 상태에서 기대되는 미래 보상의 합을 의미한다.
- Control (정책 개선, Policy Improvement):
- Prediction 결과로 나온 상태 가치 함수 Vπ(s)를 바탕으로, 각 상태에서 더 나은 행동을 선택하여 정책을 개선하는 과정이다.
- 이 단계에서는 각 상태에서 가장 좋은 행동을 선택하여 새로운 정책을 만든다.
- 정책이 개선된 후, 그 정책에 따른 상태 가치를 다시 평가하는 과정으로 돌아가면서 최적 정책을 찾아간다.

On-policy learning은 자신이 직접 시행착오를 격으면서 스스로 배우는 것에 비유를 할 수 있다. 동일한 policy인 파이에 대하여 샘플링된 경험을 따르면서 이를 통해서 학습을 하는 방식을 의미한다.
Off-policy learning은 다른이가 시행착오를 겪는것을 보면서 배우는 것에 비유를 할 수 있다. 다른 policy인 뮤에 대해서 샘플링된 경험을 따르면서 자신의 policy 파이를 학습하는 방식을 의미한다.
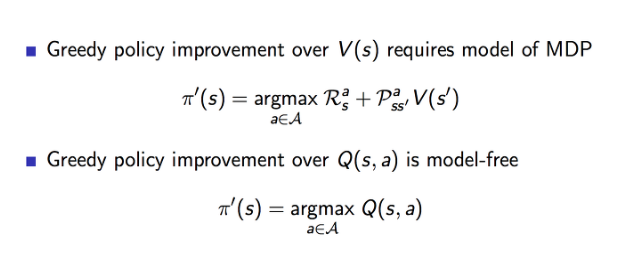
상단에 V(s)는 state에 대한 value function을 추정해야하기 때문에 MDP 모델을 사용하는 형태이다.
하단에 Q(s,a)는 s state에 대하여 a action을 취했을때 가장 큰 Q 값을 갖는 best action을 사용하게 되므로 model-free에 해당하는 방식이다.
V 대신에 Q 를 사용해서 state-action value 를 업데이트 하도록 하여 policy evaluation과 improvement를 반복한다. 최적의 q*를 찾게 되면 최적의 policy를 찾을 수 있다.

- 탐험과 활용의 균형:
- 확률 1−ϵ1 - \epsilon로 현재 가장 좋은 행동(greedy action)을 선택한다. 즉, 현재 가치 함수에서 가장 높은 보상을 줄 것으로 예상되는 행동을 선택한다.
- 확률 ϵ로 무작위로 행동을 선택한다. 이때 모든 행동은 작은 확률로라도 선택될 가능성이 있다.
- ϵ 확률로 무작위 행동을 선택하므로, 모든 행동이 비록 낮은 확률이라도 시도될 가능성이 있다. 이는 새로운 행동을 탐험하는 것을 보장해준다.
- 탐험과 활용을 조정하는 방법으로, 대부분은 가장 좋은 행동을 선택하지만, 가끔은 무작위로 행동하여 새로운 것을 탐험한다.
- ϵ이 클수록 더 많은 탐험이 이루어지고, 작을수록 더 많이 현재 좋은 행동을 선택하게 된다.


- Monte Carlo Policy Iteration은 정책 평가와 정책 개선을 교대로 수행하면서 점진적으로 최적 정책에 수렴한다.
- Monte Carlo Control은 매 에피소드마다 정책 평가와 정책 개선이 동시에 이루어지며, 더 빠르게 최적 정책으로 수렴하는 경향이 있다.

- Prediction = Policy Evaluation:
- Prediction은 주어진 정책이 얼마나 좋은지를 평가하는 과정으로, 이는 Policy Evaluation이다. 즉, 현재 정책을 따를 때 각 상태의 가치를 계산하는 과정이다.
- Control = Policy Improvement + Policy Evaluation:
- Control은 정책을 개선하는 과정인데, 이때 항상 정책 평가와 정책 개선이 교대로 일어난다.
- Policy Evaluation (eval): 현재 정책이 얼마나 좋은지를 평가하는 과정 (즉, 상태 가치를 구하는 과정).
- Policy Improvement (imp): 평가된 결과를 바탕으로, 더 나은 행동을 선택하여 정책을 개선하는 과정.

GLIE는 Greedy in the Limit with Infinite Exploration의 약자로, 무한 탐험을 하면서도 최종적으로는 탐욕적(Greedy) 정책에 수렴하는 것을 의미한다. 이는 강화학습에서 탐험과 활용을 균형 있게 처리하는 중요한 개념이다.

ε-Greedy와 GLIE:
- ε-Greedy 정책은 GLIE 조건을 만족할 수 있다. 탐험을 지속하면서도 시간이 지나면 점차 탐욕적 정책으로 수렴하게 된다.
- 예를 들어, ε-Greedy 방법에서 ε이 점차 줄어드는 경우, 초기에는 탐험을 많이 하지만, 시간이 지남에 따라 탐험을 줄이고 탐욕적인 행동을 점점 더 많이 선택하게 된다.

SARSA 알고리즘이란?
- SARSA는 State-Action-Reward-State-Action의 약자로, 각 단계에서 상태, 행동, 보상, 다음 상태, 다음 행동을 기반으로 학습하는 알고리즘이다. 이 알고리즘은 on-policy 강화학습 방법으로, 현재의 정책에 따라 행동을 선택하고 그에 따른 Q-함수를 업데이트한다.
SARSA의 작동 원리:
- S, A: 에이전트가 현재 상태 에서 행동 A를 선택한다.
- R: 그 행동을 수행한 후 보상 R을 얻는다.
- S': 에이전트는 다음 상태 S′로 전이한다.
- A': 다음 상태 S′에서 새로운 행동 A′를 선택한다.
SARSA는 이 일련의 과정(S -> A -> R -> S' -> A')을 사용해 Q-함수를 업데이트한다.
Q-함수 업데이트 식:
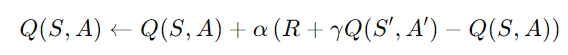


1. n-Step SARSA:
- n-Step SARSA는 몇 단계(n-step) 후의 보상을 얼마나 고려할지 결정하는 방법이다.
- n=1일 때는 일반적인 SARSA (한 단계만 고려).
- n=∞일 때는 Monte Carlo 방식으로, 전체 에피소드를 고려한다.
- 중간 단계인 n=2, 3, ...에선 해당 단계만큼 보상을 계산해 업데이트.

2. Forward View SARSA(λ):
- λ-SARSA는 여러 n-step SARSA 결과들을 가중 평균해서 업데이트한다.
- λ는 여러 단계(n-step) 사이의 가중치를 조절해주며, 이를 통해 TD(1)부터 Monte Carlo(∞)까지 다양하게 조정할 수 있다.
- 이 방식은 n-step이 아닌 모든 단계를 적절히 반영한 Q값을 계산하는 방식이다.

3. Backward View SARSA(λ):
- Eligibility Traces(자격 추적)를 사용해 이전 상태-행동 쌍에 대한 영향력을 추적하면서 업데이트한다.
- Forward View가 이론적인 설명이라면, Backward View는 실질적으로 구현 가능한 방식이다.
- δt라는 TD 오류값과 자격 추적을 이용해 과거에 있던 상태-행동 쌍의 가치를 업데이트한다.

왼쪽 그림 (Path taken):
- 에이전트가 움직인 경로를 나타낸다. 에이전트는 시작점에서 목표 지점(별 표시)까지 특정 경로를 따라 이동했다.
가운데 그림 (One-step SARSA):
- 한 단계 SARSA를 사용한 경우이다.
- 여기서 보이는 것은, 에이전트가 이동한 경로의 가치가 한 스텝만 반영된 상태이다. 즉, SARSA는 한 스텝 이후의 보상만을 반영하여 상태-행동 가치 함수를 업데이트했다.
- 에이전트가 지나간 경로에만 가치가 크게 증가했고, 이외의 경로는 거의 반영되지 않았다.
오른쪽 그림 (SARSA(λ)):
- λ 값을 사용한 SARSA(λ)로 학습한 경우이다. 여기서 λ = 0.9로 설정되었다.
- 이 경우는 에이전트가 지나간 경로 뿐만 아니라 다른 경로도 일부 반영된다. λ 값을 사용하면 여러 스텝에 걸친 보상을 더 많이 반영할 수 있기 때문이다.
- 이는 과거의 상태-행동 쌍들이 여러 스텝에 걸쳐 업데이트되어, 목표 지점에 가까워질수록 가치가 더 많이 증가하게 된다.


Q-Learning






SARSA vs. Q-Learning:
1. SARSA (State-Action-Reward-State-Action):
- On-policy 방법: SARSA는 현재 에이전트가 실제로 선택한 행동에 기반해 Q-값을 업데이트한다.
- 즉, 다음 상태에서 실제로 선택한 행동 A′A'에 대한 Q-값을 사용한다.
- 업데이트 식:
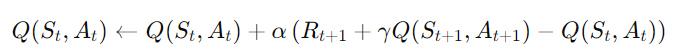
2. Q-Learning:
- Off-policy 방법: Q-Learning은 에이전트가 다음 상태에서 **가장 좋은 행동(탐욕적 행동)**을 취한다고 가정하고 Q-값을 업데이트한다.
- 즉, 실제로 선택한 행동과 상관없이, 다음 상태에서 최적의 행동을 가정하여 학습한다. 그래서 SARSA와는 달리, Q-Learning은 최적 정책을 따르는 학습 방식이라고 할 수 있다.
- 업데이트 식:
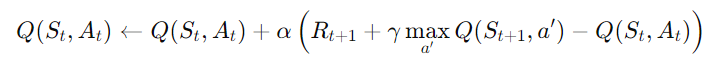
핵심 차이점:
- SARSA: 현재 정책에 따라 실제로 취한 행동을 기준으로 업데이트한다. 즉, 탐험적 행동도 반영되기 때문에 정책을 따르면서 학습하는 on-policy 방식이다.
- 따라서, 탐험적인 행동을 할 때 Q-값이 더 낮을 수 있다.
- Q-Learning: 다음 상태에서 최적의 행동을 취한다고 가정하고 업데이트한다. 탐욕적 행동을 기준으로 학습하므로 정책과 상관없이 더 나은 행동을 예측하는 off-policy 방식이다.
- 항상 최적의 Q-값을 추구하기 때문에 더 빠르게 수렴할 수 있다.
이 두 알고리즘의 차이는 실제로 선택한 행동을 기준으로 할 것인지, 최적의 행동을 기준으로 할 것인지에서 나타나는 것이다.

Cliff Walking 문제
- 목표: 에이전트는 출발점 S에서 시작하여 목적지 G에 도달해야 한다.
- 위험 요소: 에이전트가 절벽(Cliff)에 떨어지면 −100의 큰 보상을 받는다. 즉, 절벽은 피해야 한다.
- 일반적인 보상: 이동할 때마다 −1의 보상을 받는다. 즉, 최적 경로는 빠르게 목표에 도달하면서 절벽을 피하는 것이다.
SARSA와 Q-Learning의 경로 차이:
- SARSA:
- 안전한 경로를 택한다. SARSA는 on-policy 학습이기 때문에, 에이전트가 실제로 선택한 경로에 대해 학습한다.
- SARSA는 탐험적 행동을 고려하며, 절벽 근처에서 위험한 경로를 피하는 방향으로 학습되기 때문에, 비교적 안전한 경로를 택하게 된다.
- Q-Learning:
- 최적 경로를 찾는다. Q-Learning은 off-policy 학습이므로, 에이전트는 다음 상태에서 항상 최적의 행동을 한다고 가정하고 학습한다.
- Q-Learning은 보상을 극대화하기 위해 절벽 바로 옆을 지나가는 최단 경로를 찾는다. 이 경로는 빠르지만, 탐험 중에는 절벽에 떨어질 위험이 있다.
그래프 해석:
- X축: 에피소드 수 (학습이 진행될수록 에이전트는 더 많은 경험을 쌓는다).
- Y축: 에피소드 당 보상 (값이 높을수록 더 나은 성과).
- SARSA: 에피소드가 진행될수록 안정적으로 보상을 얻는다. 초기에는 탐험 중에 절벽에 떨어질 수도 있지만, 시간이 지나면 안전한 경로를 학습하게 된다.
- Q-Learning: Q-Learning은 최적의 경로를 찾는 동안 더 많이 절벽에 떨어지므로 보상이 더 낮게 시작된다. 하지만 시간이 지남에 따라 최적 경로를 학습하면서도 일부 절벽에 떨어지는 경우가 존재해 변동이 크다.

Relationship Between DP and TD

1.1 Full Backup (DP) vs Sample Backup (TD):
- Full Backup (DP): 동적 프로그래밍은 모델 기반으로 모든 상태에 대해 전이 확률을 사용하여 계산한다. 즉, 모든 가능한 다음 상태를 고려해 벨만 방정식을 사용해 값을 업데이트한다.
- Sample Backup (TD): 템포럴 디퍼런스는 모델 프리 방식으로 경험에서 샘플링된 데이터를 사용해 값을 업데이트한다. TD 학습은 한 번에 하나의 상태 전이를 고려해 업데이트한다.
1.2 각 학습 방식에 해당하는 알고리즘:
- Value Function:
- DP에서는 Iterative Policy Evaluation으로 상태 가치 V(s)를 평가한다.
- TD 학습에서는 경험을 바탕으로 TD Learning을 사용해 V(s)를 업데이트한다.
- Q-Function:
- DP에서는 Q-Policy Iteration을 통해 정책을 기반으로 상태-행동 가치 Q(s,a)를 평가한다.
- TD 학습에서는 SARSA를 사용해 현재 정책을 따르는 상태-행동 가치 Q(s,a)를 업데이트한다.
- Optimal Q-Function:
- DP에서는 Q-Value Iteration을 통해 최적의 상태-행동 가치 함수 Q∗(s,a)를 계산한다.
- TD 학습에서는 Q-Learning을 통해 최적의 상태-행동 가치 함수 Q∗(s,a)를 학습한다.

2.1 Value Function 업데이트 방식:
- DP (Full Backup): 벨만 기대 방정식을 사용하여 다음 상태의 모든 전이 확률을 고려해 값을 계산한다.
- TD (Sample Backup): 하나의 샘플 데이터를 기반으로 업데이트를 한다.
2.2 Q-Function 업데이트 방식:
- DP (Full Backup): 모든 가능한 다음 상태와 행동에 대해 기대값을 계산한다.
- TD (Sample Backup): SARSA를 통해 실제 행동과 결과에 따라 Q-값을 업데이트한다.
2.3 Optimal Q-Function 업데이트 방식:
- DP (Full Backup): 최적 행동을 고려해 모든 상태 전이에 대해 업데이트한다.
- TD (Sample Backup): Q-Learning을 통해 샘플된 경험에서 최적의 행동을 찾아 업데이트한다.
'AI > RL' 카테고리의 다른 글
| [RL] 4-1 Value Function Approximation (0) | 2024.10.13 |
|---|---|
| [RL] 3-1 Model-Free Prediction - (TD lambda) (2) | 2024.10.12 |
| [RL] 3-1 Model-Free Prediction - (TD) (0) | 2024.10.09 |
| [RL] 3-1 Model-Free Prediction - (MC) (0) | 2024.10.09 |
| [RL] 2-2 Planning by Dynamic Programming (0) | 2024.10.09 |