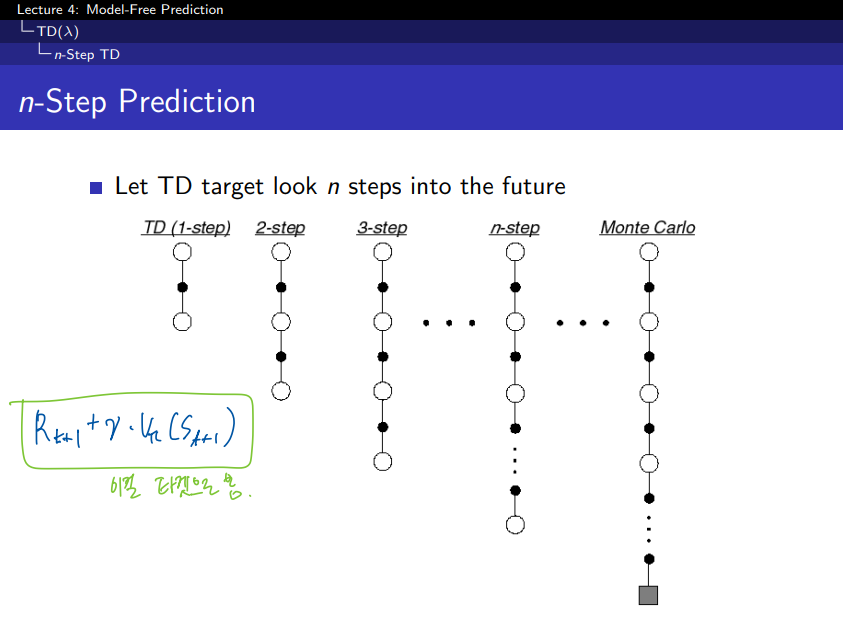
1. step TD의 step을 증가시켜 나가면서 n 까지 보게 되면 n step TD로 일반화를 할 수 있습니다. 만약 step이 무한대에 가깝게 되면 MC와 동일하게 될 것 이다.
2. step TD 에서의 업데이트 방식은 첫번째 보상과 + 두번째 보상 + 두번째 상태에서의 value function 으로 업데이트가 된다.
TD(1-step)과 n-Step의 차이
- TD(1-step): 한 단계 후의 보상과 다음 상태의 가치 함수만을 기반으로 업데이트를 수행한다.
- 업데이트 식:
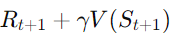
-
- 즉, t+1시점에서의 보상과 다음 상태의 가치 V(St+1)를 이용해 현재 상태 StS_t의 가치를 업데이트한다.
- n-Step TD: 한 단계가 아니라, n단계 후의 보상까지 고려한다.
- n-Step TD에서는 n번째 시점까지의 보상을 합산해 업데이트에 사용한다.
- 예를 들어, 3-Step TD의 경우:
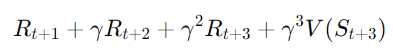
- 3단계 후의 보상까지 고려하고, 그 이후에는 가치 함수 V(St+3)를 사용한다.
- Monte Carlo: Monte Carlo는 전체 에피소드가 끝난 후에 총 보상(Return)을 계산해 업데이트를 수행한다. n이 매우 커져서 에피소드 전체를 다 본다고 생각하면 Monte Carlo가 된다.
"이걸 타겟으로 봄"의 의미
- 여기서 "타겟"은 업데이트의 목표값을 의미한다. 즉, 각 상태 St의 가치를 계산할 때, 업데이트의 목표값으로 미래의 보상과 미래 상태의 가치 함수를 사용한다는 것이다.
- TD(1-step)에서는 한 단계 후의 보상과 다음 상태의 가치 함수 V(St+1)를 타겟으로 삼는다.
- n-Step TD에서는 n단계 후까지의 보상을 모두 합산하고, 마지막 상태의 가치 함수를 타겟으로 삼는다.

n step TD에서의 value 함수는 n step에서 얻은 총 보상에서 기존 value 함수값과의 차이를 알파만큼 가중치하여 더함으로서 업데이트가 되게 된다.
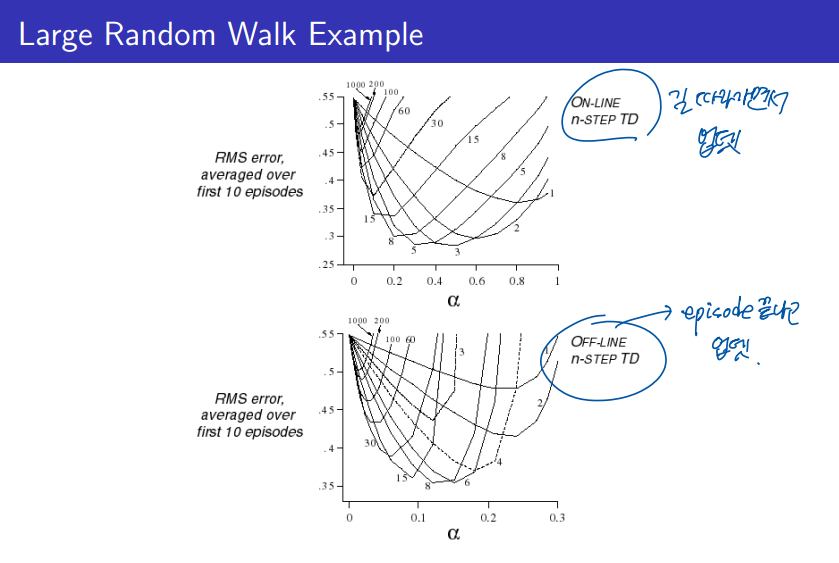
그럼 n 이 몇일 때가 가장 최고의 결과를 나타낼까? 그에 대한 실험이 위의 그래프이다.
실시간 업데이트 하는 온라인 방식, 에피소드 완료후 업데이트하는 오프라인 방식에서 비슷한 결과로 나타나며, n 이 커질수록 에러가 큰것을 볼 수 있다. 그래프를 보니 3~5 의 step size 혹은 6~8 의 step size가 좋은것 같다.
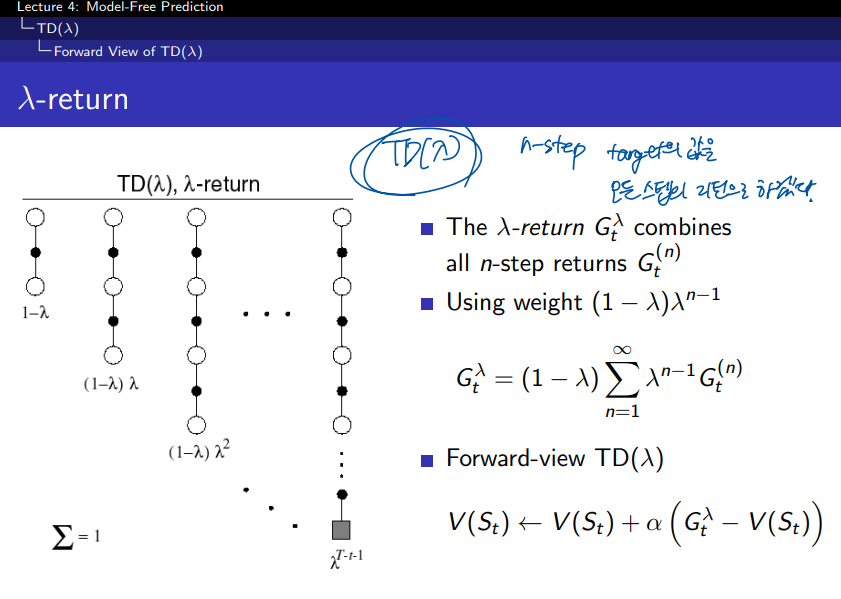

여기서 람다 보상은 모든 n step까지의 가중평균된 보상이다. 기존에 n step에서 사용한 보상은 총합이었는데 람다 방식처럼 평균을 사용하는 방식은 오류를 더 낮춰줄 수 있다.
람다의 총합이 1이 되도록 하기 위해서 (1 - 람다) 계수로 노멀라이즈를 하여 0부터 1까지의 값을 갖도록 한다. 그리하여 이 람다는 n step이 커질수록 보상에 대한 값(중요도)을 감소시키게 작용한다.
람다가 0에 가까울수록 현재를 중요하게 보고, 람다가 1에 가까울수록 미래를 중요하게 본다.
λ가 작을수록 짧은 단계의 보상에 더 많은 가중치를 두고, λ가 클수록 더 긴 단계의 보상을 고려한다.
λ의 역할
- λ는 0에서 1 사이의 값으로, TD(1-step)과 Monte Carlo 사이를 조정한다.
- λ = 0이면, TD(1-step)이 되고, 가장 가까운 미래의 보상만 사용하여 상태 가치를 업데이트한다.
- λ = 1이면, Monte Carlo 방식이 되고, 전체 에피소드가 끝난 후의 총 보상을 사용하여 상태 가치를 업데이트한다.
- 0 < λ < 1에서는 여러 n-step들을 가중 평균하여, TD와 Monte Carlo의 중간 방식으로 학습이 이루어진다.
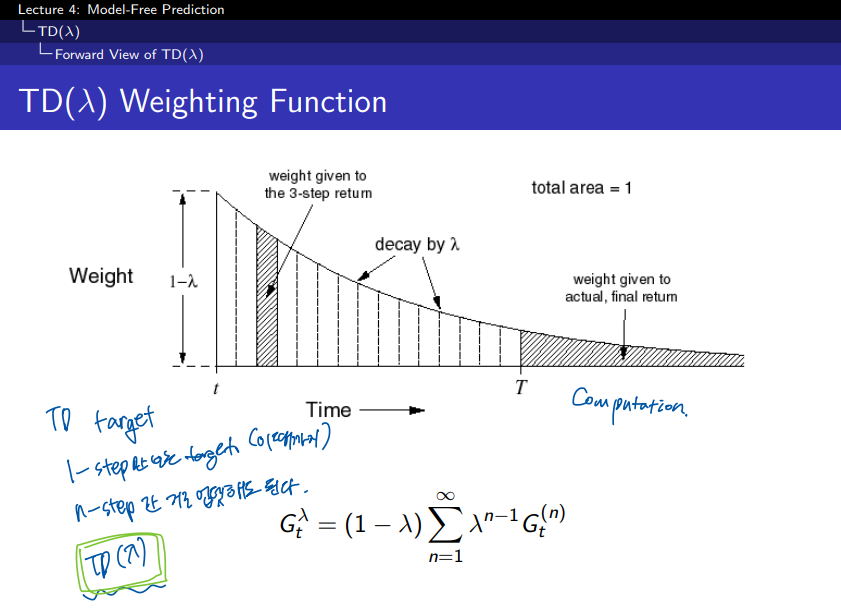
step 시간이 흐를수록 weight 가 지수형태로 감소를 하는 것을 볼 수 있다. 그리고 이들의 총합은 1이 된다. 지수형태의 가중치를 사용하는 것이 알고리즘의 연산에 효율성을 주고 메모리를 덜 사용하게 되는 이점이 있다고 한다.
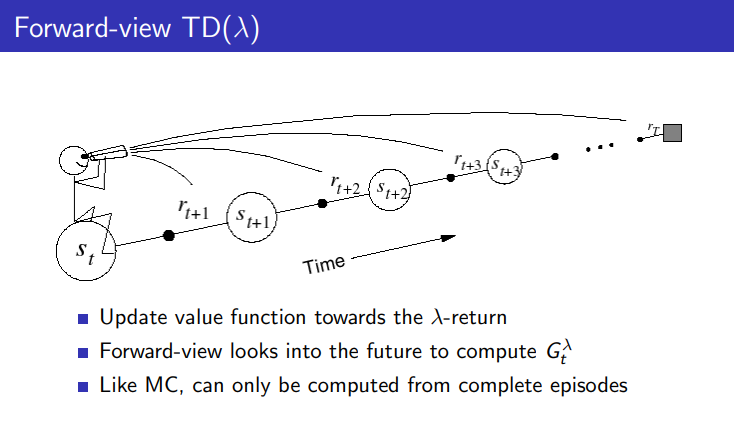
value 함수가 업데이트 되는 과정을 도식화한것이다. 동일하게 n step 까지 도달하고 나서 얻은 보상들을 람다 보상을 구해서 업데이트 하게 된다.
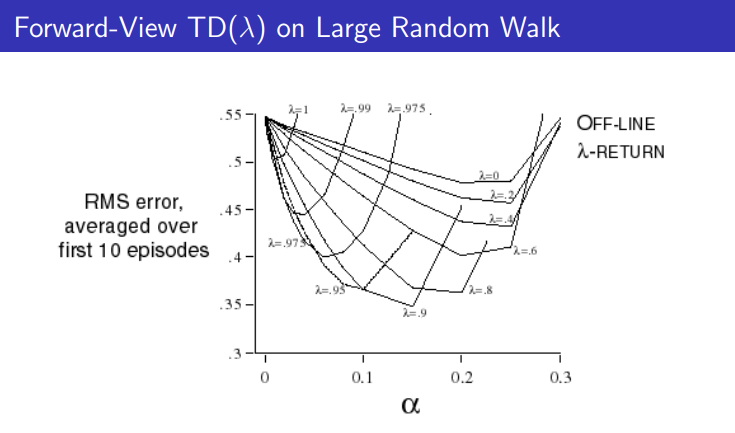
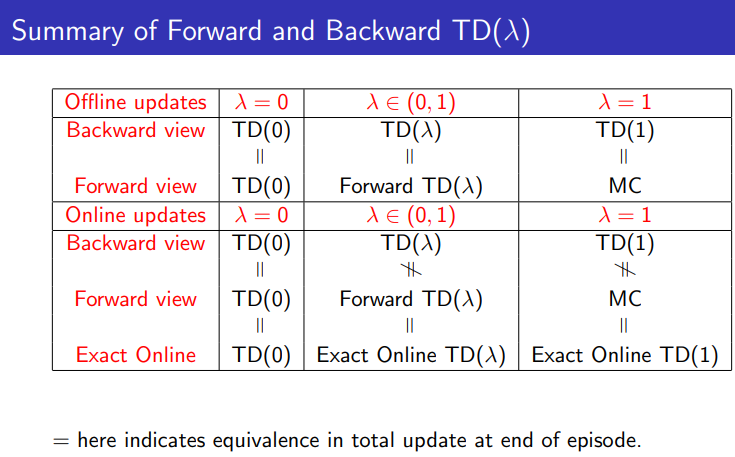
그래프를 보니 람다가 .9 정도에서 결과가 좋은 것을 볼 수 있다. 람다가 1일때에는 MC가 되고 0일 경우에는 TD(0)가 된다. bias와 variance의 trade off를 고려해서 적절한 값으로 사용하면 좋을 것 이다.

1. Forward View:
- 이론적인 관점을 제공한다.
- Forward View에서는 n-step return을 가중 평균하여 업데이트를 수행하는 방식으로 λ-return을 계산한다. 즉, 각 단계의 보상을 여러 단계로 나누어 가중치를 적용하고, 이를 기반으로 상태 가치를 업데이트한다.
- Forward View는 직관적으로 이해하기 좋고, 이론적으로 TD(λ)가 어떻게 동작하는지 설명하는데 유용하다. 하지만 실질적으로 이 방식은 에피소드가 끝나야 계산할 수 있다.
2. Backward View:
- 컴퓨터적으로 구현 가능한 방식을 제공한다.
- Backward View에서는 온라인 학습이 가능하며, 각 스텝마다 상태 가치를 업데이트한다. 즉, 매 시간 단계에서 보상과 상태의 정보를 바로바로 반영하며 업데이트가 이루어진다.
- 이 방식은 온라인 학습이 가능하게 만들어주며, 모든 상태에 대한 추적기(trace)를 유지하면서 업데이트를 수행한다.
- 예를 들어, 특정 상태에서 보상을 얻으면, 그 상태뿐만 아니라 이전의 여러 상태들도 동시에 업데이트될 수 있다
- TD(λ)는 Backward View에 의해 실시간으로 매 스텝마다 업데이트될 수 있으며, 이는 incomplete sequences (완전하지 않은 시퀀스)에서도 작동할 수 있다는 것을 의미한다. 즉, 에피소드가 끝나지 않아도 매 시간 단계마다 학습을 할 수 있다.

예제를 보면 위에서 번개가 발생한 이유가 종 때문일까? 라이트 때문일까요? 자주 발생한 것이 영향이 큰지 최근에 발생한 것이 영향이 큰지를 결합하여 사용할 수 있다.
하나의 특정한 state를 방문하는 횟수에 따라서 Eligibility traces를 해보면 위 그래프와 같이 된다.

이를 적용해보면 각 state마다 업데이트가 발생이 될때 TD 에러의 비율 만큼 업데이트를 가중적용하는 것으로 할 수 있다. 이것은 에피소드의 길이보다 짧은 기억을 하는 단기 메모리 같은 역할을 한다.

람다는 얼마나 빨리 값을 감소시키는가를 의미합니다. 람다가 0의 값이 되면 완전 가파르게 decay가 발생할 것 이다. 결국 현재 state의 value 함수만 업데이트가 되며 이는 TD(0)와 동일한 방식이 된다.

반대로 람다가 1이 되면 전체 에피소드를 모두 커버하게 된다. 그래서 오프라인 업데이트와 같이 될 것이고 이는 MC와 같은 방식이 된다.
참고: https://daeson.tistory.com/334 [대소니:티스토리]
'AI > RL' 카테고리의 다른 글
| [RL] 4-1 Value Function Approximation (0) | 2024.10.13 |
|---|---|
| [RL] 3-2 Model-Free Control (1) | 2024.10.12 |
| [RL] 3-1 Model-Free Prediction - (TD) (0) | 2024.10.09 |
| [RL] 3-1 Model-Free Prediction - (MC) (0) | 2024.10.09 |
| [RL] 2-2 Planning by Dynamic Programming (0) | 2024.10.09 |

1. step TD의 step을 증가시켜 나가면서 n 까지 보게 되면 n step TD로 일반화를 할 수 있습니다. 만약 step이 무한대에 가깝게 되면 MC와 동일하게 될 것 이다.
2. step TD 에서의 업데이트 방식은 첫번째 보상과 + 두번째 보상 + 두번째 상태에서의 value function 으로 업데이트가 된다.
TD(1-step)과 n-Step의 차이
- TD(1-step): 한 단계 후의 보상과 다음 상태의 가치 함수만을 기반으로 업데이트를 수행한다.
- 업데이트 식:
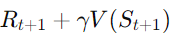
-
- 즉, t+1시점에서의 보상과 다음 상태의 가치 V(St+1)를 이용해 현재 상태 StS_t의 가치를 업데이트한다.
- n-Step TD: 한 단계가 아니라, n단계 후의 보상까지 고려한다.
- n-Step TD에서는 n번째 시점까지의 보상을 합산해 업데이트에 사용한다.
- 예를 들어, 3-Step TD의 경우:
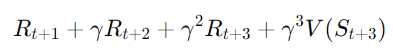
- 3단계 후의 보상까지 고려하고, 그 이후에는 가치 함수 V(St+3)를 사용한다.
- Monte Carlo: Monte Carlo는 전체 에피소드가 끝난 후에 총 보상(Return)을 계산해 업데이트를 수행한다. n이 매우 커져서 에피소드 전체를 다 본다고 생각하면 Monte Carlo가 된다.
"이걸 타겟으로 봄"의 의미
- 여기서 "타겟"은 업데이트의 목표값을 의미한다. 즉, 각 상태 St의 가치를 계산할 때, 업데이트의 목표값으로 미래의 보상과 미래 상태의 가치 함수를 사용한다는 것이다.
- TD(1-step)에서는 한 단계 후의 보상과 다음 상태의 가치 함수 V(St+1)를 타겟으로 삼는다.
- n-Step TD에서는 n단계 후까지의 보상을 모두 합산하고, 마지막 상태의 가치 함수를 타겟으로 삼는다.

n step TD에서의 value 함수는 n step에서 얻은 총 보상에서 기존 value 함수값과의 차이를 알파만큼 가중치하여 더함으로서 업데이트가 되게 된다.

그럼 n 이 몇일 때가 가장 최고의 결과를 나타낼까? 그에 대한 실험이 위의 그래프이다.
실시간 업데이트 하는 온라인 방식, 에피소드 완료후 업데이트하는 오프라인 방식에서 비슷한 결과로 나타나며, n 이 커질수록 에러가 큰것을 볼 수 있다. 그래프를 보니 3~5 의 step size 혹은 6~8 의 step size가 좋은것 같다.


여기서 람다 보상은 모든 n step까지의 가중평균된 보상이다. 기존에 n step에서 사용한 보상은 총합이었는데 람다 방식처럼 평균을 사용하는 방식은 오류를 더 낮춰줄 수 있다.
람다의 총합이 1이 되도록 하기 위해서 (1 - 람다) 계수로 노멀라이즈를 하여 0부터 1까지의 값을 갖도록 한다. 그리하여 이 람다는 n step이 커질수록 보상에 대한 값(중요도)을 감소시키게 작용한다.
람다가 0에 가까울수록 현재를 중요하게 보고, 람다가 1에 가까울수록 미래를 중요하게 본다.
λ가 작을수록 짧은 단계의 보상에 더 많은 가중치를 두고, λ가 클수록 더 긴 단계의 보상을 고려한다.
λ의 역할
- λ는 0에서 1 사이의 값으로, TD(1-step)과 Monte Carlo 사이를 조정한다.
- λ = 0이면, TD(1-step)이 되고, 가장 가까운 미래의 보상만 사용하여 상태 가치를 업데이트한다.
- λ = 1이면, Monte Carlo 방식이 되고, 전체 에피소드가 끝난 후의 총 보상을 사용하여 상태 가치를 업데이트한다.
- 0 < λ < 1에서는 여러 n-step들을 가중 평균하여, TD와 Monte Carlo의 중간 방식으로 학습이 이루어진다.

step 시간이 흐를수록 weight 가 지수형태로 감소를 하는 것을 볼 수 있다. 그리고 이들의 총합은 1이 된다. 지수형태의 가중치를 사용하는 것이 알고리즘의 연산에 효율성을 주고 메모리를 덜 사용하게 되는 이점이 있다고 한다.

value 함수가 업데이트 되는 과정을 도식화한것이다. 동일하게 n step 까지 도달하고 나서 얻은 보상들을 람다 보상을 구해서 업데이트 하게 된다.

그래프를 보니 람다가 .9 정도에서 결과가 좋은 것을 볼 수 있다. 람다가 1일때에는 MC가 되고 0일 경우에는 TD(0)가 된다. bias와 variance의 trade off를 고려해서 적절한 값으로 사용하면 좋을 것 이다.

1. Forward View:
- 이론적인 관점을 제공한다.
- Forward View에서는 n-step return을 가중 평균하여 업데이트를 수행하는 방식으로 λ-return을 계산한다. 즉, 각 단계의 보상을 여러 단계로 나누어 가중치를 적용하고, 이를 기반으로 상태 가치를 업데이트한다.
- Forward View는 직관적으로 이해하기 좋고, 이론적으로 TD(λ)가 어떻게 동작하는지 설명하는데 유용하다. 하지만 실질적으로 이 방식은 에피소드가 끝나야 계산할 수 있다.
2. Backward View:
- 컴퓨터적으로 구현 가능한 방식을 제공한다.
- Backward View에서는 온라인 학습이 가능하며, 각 스텝마다 상태 가치를 업데이트한다. 즉, 매 시간 단계에서 보상과 상태의 정보를 바로바로 반영하며 업데이트가 이루어진다.
- 이 방식은 온라인 학습이 가능하게 만들어주며, 모든 상태에 대한 추적기(trace)를 유지하면서 업데이트를 수행한다.
- 예를 들어, 특정 상태에서 보상을 얻으면, 그 상태뿐만 아니라 이전의 여러 상태들도 동시에 업데이트될 수 있다
- TD(λ)는 Backward View에 의해 실시간으로 매 스텝마다 업데이트될 수 있으며, 이는 incomplete sequences (완전하지 않은 시퀀스)에서도 작동할 수 있다는 것을 의미한다. 즉, 에피소드가 끝나지 않아도 매 시간 단계마다 학습을 할 수 있다.

예제를 보면 위에서 번개가 발생한 이유가 종 때문일까? 라이트 때문일까요? 자주 발생한 것이 영향이 큰지 최근에 발생한 것이 영향이 큰지를 결합하여 사용할 수 있다.
하나의 특정한 state를 방문하는 횟수에 따라서 Eligibility traces를 해보면 위 그래프와 같이 된다.

이를 적용해보면 각 state마다 업데이트가 발생이 될때 TD 에러의 비율 만큼 업데이트를 가중적용하는 것으로 할 수 있다. 이것은 에피소드의 길이보다 짧은 기억을 하는 단기 메모리 같은 역할을 한다.

람다는 얼마나 빨리 값을 감소시키는가를 의미합니다. 람다가 0의 값이 되면 완전 가파르게 decay가 발생할 것 이다. 결국 현재 state의 value 함수만 업데이트가 되며 이는 TD(0)와 동일한 방식이 된다.

반대로 람다가 1이 되면 전체 에피소드를 모두 커버하게 된다. 그래서 오프라인 업데이트와 같이 될 것이고 이는 MC와 같은 방식이 된다.

참고: https://daeson.tistory.com/334 [대소니:티스토리]
'AI > RL' 카테고리의 다른 글
| [RL] 4-1 Value Function Approximation (0) | 2024.10.13 |
|---|---|
| [RL] 3-2 Model-Free Control (1) | 2024.10.12 |
| [RL] 3-1 Model-Free Prediction - (TD) (0) | 2024.10.09 |
| [RL] 3-1 Model-Free Prediction - (MC) (0) | 2024.10.09 |
| [RL] 2-2 Planning by Dynamic Programming (0) | 2024.10.09 |