Dynamic Programming
복잡한 문제를 풀기 위한 방법으로 큰 문제를 작은 subproblem들로 쪼개서 문제를 푸는 방법을 뜻한다.

하나는 Optimal substructure 로서 최적화를 할 수 있다는 것인데 하나의 문제를 2개 이상의 하위문제로 쪼개고 각각을 최적화하게 되면 원래의 문제도 최적화 할 수 있다는 것이다.
또 하나는 Overlapping subproblems 인데 서브문제들이 여러번 반복적으로 나타나기 때문에 하나의 서브문제를 해결하고 이 결과를 저장했다가 다시 사용하는 것이 가능하다는 것이다.
이 두가지 특성이 MDP에서도 동일하게 적용이 되고 Bellman equation 과 value function 이 대표적인 특성을 가지고 있다.
Bellman equation 이 각 step 별로 연산을 할 수 있도록 해주고 각 step (state) 에서의 value function 은 저장되었다가 다시 연산할때 사용되게 된다.

Dynamic Programming 은 MDP의 모든 상황에 대한 것을 이미 알고 있다고 가정한다. 그렇기 때문에 planning 을 할 수 있게 되는 것이다. 만약 모든 상황이 아닌 일부만 알고 있다면 planning을 할 수 없다.
MDP와 policy를 입력으로 하여 value function을 찾아내는 것이 prediction 과정이다.
그리고 MDP를 입력으로 하여 기존의 value function을 더욱 최적화 하는 것이 control 과정이다.
최종적으로 policy 는 value function을 통해서 생성할 수 있기 때문에 최적화된 value function을 통해서 최적화된 optimal policy를 찾을 수 있게 된다.
Policy Evaluation

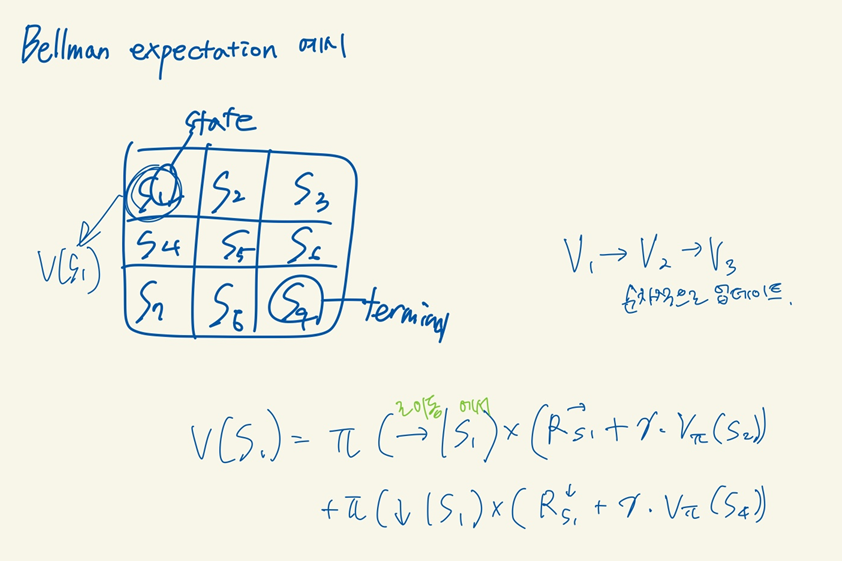
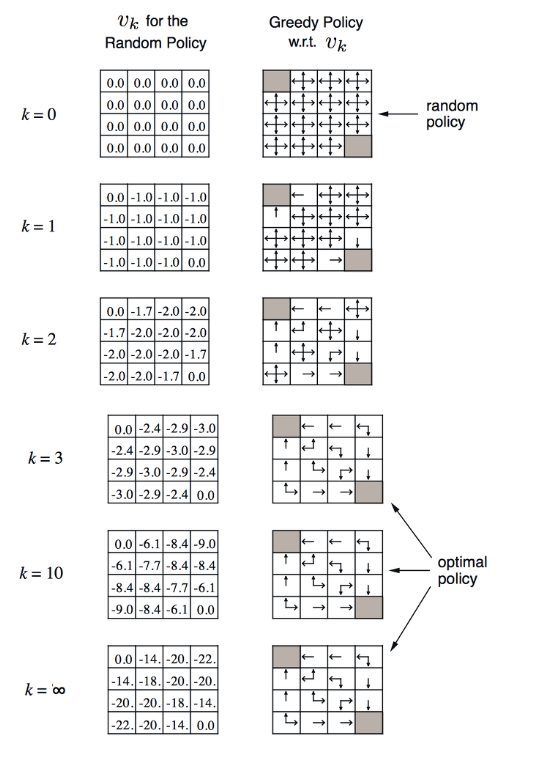
k가 0일때는 모든 states의 value가 0으로 초기화 되어 시작이 된다. 각각의 states에 대한 value function의 연산이 되고 다음 k 가 1이 되면 terminal states가 아닌 states들의 value 값이 -1로 되며 이때의 value를 이용해서 policy를 구해보면 오른쪽과 같이 행동이 표기가 된다.
이렇게 반복되면서 k 가 3이상이 되면 policy가 최적이 되면서 value 값이 업데이트가 되는 것을 볼 수 있다. k 가 무한대로 가면 value 값도 최적화가 되는 것을 볼 수 있다.
어느 states에서 시작을 하더라도 현재의 state 보다 큰 값을 가지는 state로 이동을 하게 될 것이고 그 행동을 자연스럽게 policy를 따르게 된다. 그리고 계속 이 policy를 따라 이동을 하다보면 terminal state로 가게 되는 것을 볼 수 있다.
Policy Iteration
policy를 더 좋게 업데이트를 할 수 있는 방법이 없을까? 에 대한 문제를 해결하기 위해서 위와 같이 2가지의 접근 방식을 취하게 된다.
먼저 현재의 policy를 통해서 value function을 찾는것을 evaluate라고 한다.
그리고 이 value 값과 action에 대한 value값을 비교하여 더 좋은 policy를 찾아가는 과정을 improve 라고 한다.
이 두가지 과정을 반복하여 수행하게 되면 policy와 value가 수렴하게 되고 그때가 최적화 된 policy와 value라고 할 수 있다.
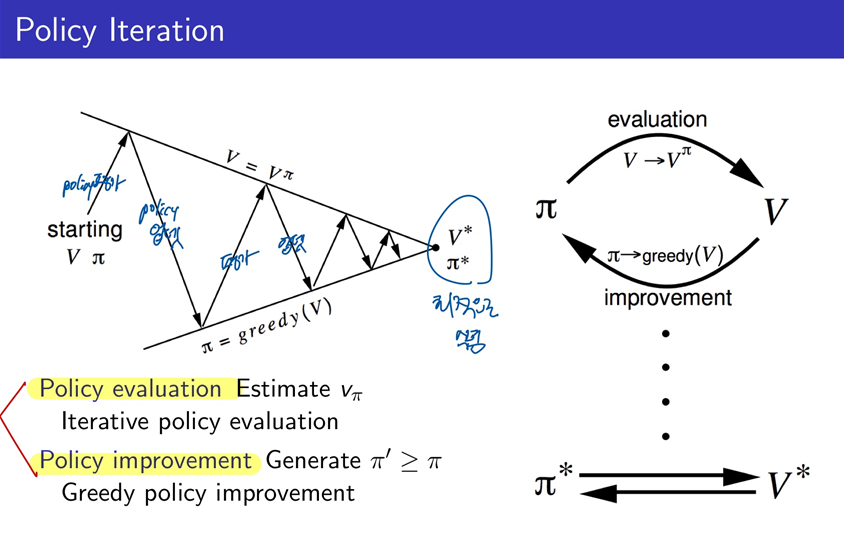
evaluation이 수행이 되면서 v 가 업데이트 되어 변경이 되고, 그에 따라 policy를 더 좋은 policy로 업데이트하는 improvement가 수행이 되는 것을 반복적으로 하면서 v*와 PI*로 수렴하게 되는 것을 도식화 하여 보여주고 있다.
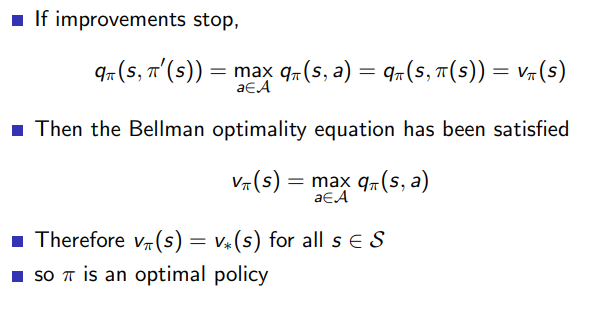
policy improve 과정이 반복되면서 어느정도 수렴이 하게 되면, 위와 같이 q의 값과 v의 값이 같아지는 지점이 오게 될 것이다. 이때의 v와 policy는 최적화된 상태라고 할 수 있고 이때의 policy를 optimal policy라고 할 수 있다.

이렇게 policy iteration이 계속되면 언제까지 반복해야할까? 끝까지 수렴할때까지 할 수도 있겠지만 너무 오래걸릴 수 있기 때문에 value function의 변화량이 특정한 값 이하가 되면 stop을 하도록 할 수 있다. 또는 매번 iteration마다 policy improve 를 하면 비용이 커지므로 간단하게 k 가 몇번 반복된 이후에 한번 improve 하도록 할수도 있다.
이러한 방법들은 optimal policy를 좀더 빨리 찾을 수 있도록 하는 성능을 개선하는데 유용하다.
Value Iteration

optimal policy는 첫번째 action이 최적화 되는 부분과 그 다음 전체적인 action들이 최적화 되는 부분으로 나누어 볼 수 있다. 첫번째 action이 잘 선택이 되었다면 (첫 단추가 잘 끼어졌다면) 이후의 다음 action들도 최적화될 것으로 생각할 수 있다.
그러므로 어떤 state s에서 optimal value가 되었다면 다음 state s'에서도 optimal value가 되었다고 볼 수 있다. 그리고 s' 에서의 optimal value를 찾았다면 이전상태인 s에서의 optimal value도 찾을 수 있게 된다. 이렇게 마지막 step에서 받은 보상이 뒤로 전달이 되면서 업데이트가 된다.
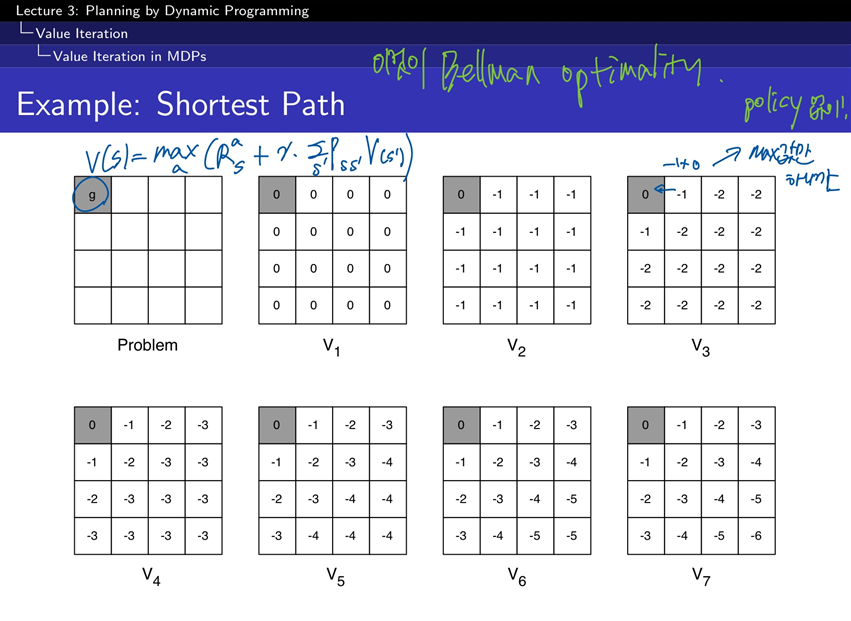
value가 업데이트가 되는 과정을 보면 위와 같이 된다. 앞에서 본 예제에서의 환경에서 한번 step을 이동할때 보상을 -1을 받았기 때문에 위와 같이 마이너스 값이 멀어지면서 커지는 값을 가지게 된다.
***********************************
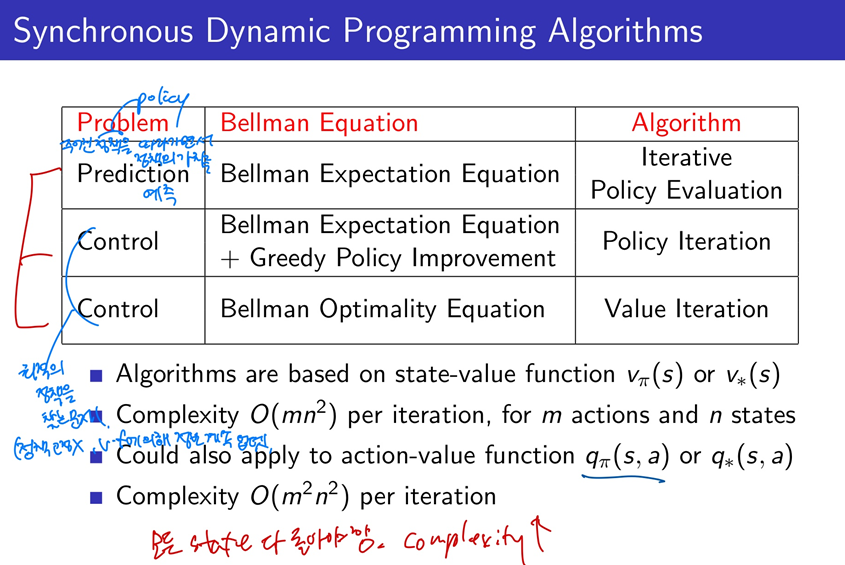
전체적으로는 policy iteration과 비슷하고 다른 부분은 synchronous backup에서 업데이트를 할때 argmax를 사용하는 것이 아니라 max를 사용해서 한번에 처리가 된다는 것입니다. 그래서 policy를 매번 업데이트 하지 않아도 되게 됩니다.

Asynchronous Dynamic Programming
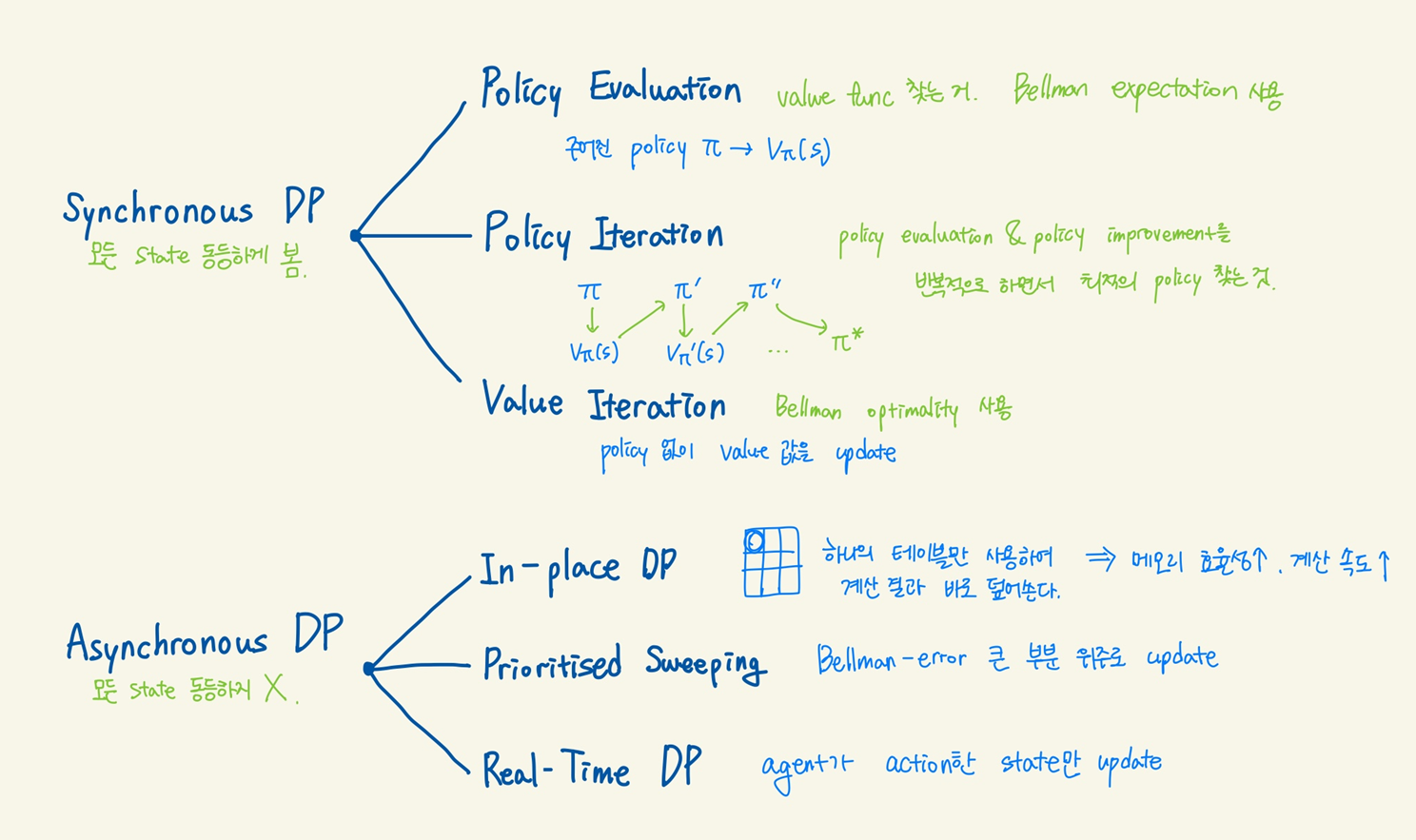
지금까지 배운 동기화 방식과 다르게 이제는 비동기 방식에 대해 배워보자. Asynchronous Dynamic Programming 은 병렬로 back up이 되는 방식이고 이러한 방식은 연산을 줄이고 수렴을 빠르게 할 수 있다.
In-Place Dynamic Programming

in-place value iteration은 v 값을 하나를 사용해서 처리하기 때문에 불필요한 복사과정이 없습니다. 그래서 더욱 빠르고 효과적으로 업데이트가 되지만 상대적으로 조금 불안정하게 업데이트가 되게 됩니다.
- In-Place Dynamic Programming에서는 하나의 테이블만 사용하여 계산 결과를 바로 덮어쓴다. 이 방식은 메모리 효율성이 높고, 계산이 더 빠르게 진행될 수 있다.
- 다만, 계산된 값이 즉시 다른 상태의 계산에 영향을 미칠 수 있기 때문에 일관성이 조금 떨어져서 값이 수렴하는 과정이 불안정해질 수 있다. 즉, 업데이트 중간에 참조하는 값들이 시점마다 달라질 수 있다.
Prioritised Sweeping

prioritised sweeping 은 Bellman error가 크게 남아있는 states를 backup에 우선순위를 주어 처리되도록 합니다. 방문횟수가 많아지면 업데이트가 최적화에 가깝게 잘되겠지만 방문횟수가 낮은 상태에서는 error가 커지게 될 것이기 때문에 더 많이 업데이트를 하도록 해줍니다.
Real-Time Dynamic Programming

- Real-Time DP는 에이전트가 실제 환경에서 학습을 진행하며, 상태와 행동의 가치를 업데이트하는 방식이다.
- 일반적인 Dynamic Programming은 모든 상태에 대해 반복적으로 값을 업데이트하지만, Real-Time DP는 방문한 상태들만 업데이트한다. 즉, 에이전트가 탐험한 경로에 있는 상태들만 학습하며, 이를 통해 불필요한 계산을 줄이고 효율성을 높인다.
- 매 시간 단계마다 에이전트가 특정 상태에 도달하면, 그 상태의 가치(또는 Q 값)를 업데이트하고 다음 상태로 이동하면서 반복한다.

이러한 DP은 Full-Width Backup이라고하는데 강화학습에서 모든 상태와 행동의 가치를 업데이트하는 방식이다. 하지만 이 방식에는 몇 가지 어려움이 있다
이러한 방식은 space가 커지면 커질수록 연산에 시간이 오래걸리고 수렴이 어려워지게 되고 차원이 커지면 커질수록 차원의 저주가 발생하여 어려움이 생기는 단점이 있다.

- Sample Backup은 방문한 상태와 행동의 샘플만 사용하여 가치를 업데이트하는 방식이다. 즉, 경험한 경로에 있는 상태들만 선택적으로 업데이트한다.
- 이를 통해 계산 비용과 메모리 사용량을 크게 줄일 수 있다. 필요할 때마다 샘플을 기반으로 학습하므로, 전체 상태 공간을 전부 다루지 않아도 된다.
- 대표적인 예로 Monte Carlo(MC) 방법이나 Temporal Difference 학습(TD)가 Sample Backup의 방식이다.
참고: https://daeson.tistory.com/325 [대소니:티스토리]
'AI > RL' 카테고리의 다른 글
| [RL] 3-1 Model-Free Prediction - (TD lambda) (2) | 2024.10.12 |
|---|---|
| [RL] 3-1 Model-Free Prediction - (TD) (0) | 2024.10.09 |
| [RL] 3-1 Model-Free Prediction - (MC) (0) | 2024.10.09 |
| [RL] 2-1 Markov Decision Processes (3) | 2024.09.29 |
| [RL] 1-1 Introduction to Reinforcement Learning (4) | 2024.09.27 |