[논문] An Efficient Fuzzy Stream Clustering MethodBased on Granular-Ball Structure

 

제목 키워드 설명

 

• Fuzzy Clustering: Fuzzy clustering은 데이터가 여러 군집에 동시에 속할 수 있도록 허용하는 방법이다. 이는 일반적인 클러스터링 기법과 달리, 데이터 포인트가 하나의 군집에만 속하는 것이 아니라, 여러 군집에 소속될 수 있는 가능성을 제공한다.
• Stream Clustering: Stream clustering은 데이터가 연속적으로 입력되는 스트리밍 데이터 환경에서 실시간으로 데이터를 클러스터링하는 기술이다. 이런 데이터는 저장이 어렵기 때문에 실시간으로 처리하고 클러스터를 형성해야 한다.
• Granular-Ball Structure: 이 용어는 데이터 포인트를 보다 효율적으로 처리하기 위한 구조를 나타낸다. "Granular"라는 개념은 데이터 집합을 보다 작은 단위로 나누어 처리하는 기법이고, "Ball"은 공간에서의 특정 영역을 나타낼 수 있다.

abstract

현재의 데이터 스트림 클러스터링 알고리즘들은 온라인 및 오프라인 단계에서 모두 효율성이 낮고, 개념 변화(concept drift)로 인해 발생하는 클러스터 경계 겹침 문제를 해결하기 힘들다. 구체적으로, 온라인 단계에서 대부분의 기존 데이터 스트림 클러스터링 알고리즘은 새로 도착하는 샘플마다 이를 스캔하고 적절한 마이크로 클러스터에 삽입해야 한다. 오프라인 클러스터링에서는 보통 모든 샘플 포인트를 입력으로 요구한다. 더욱이, 대부분의 데이터 스트림 클러스터링 알고리즘은 개념 변화로 인한 클러스터 경계 겹침 문제를 효과적으로 처리하지 못한다.

 

마이크로 클러스터란?

마이크로 클러스터는 일종의 임시 그룹으로, 데이터를 "대충 비슷한 것들끼리" 먼저 묶어두는 방식이다. 실시간으로 데이터가 빠르게 들어오니까, 데이터를 일일이 세밀하게 분류할 시간이 없을 때 대충 과일처럼 보이는 것들을 하나로 묶어두는 것 이다.

1. 마이크로 클러스터: 실시간으로 빠르게 들어오는 데이터들을 대략적으로 비슷한 것들끼리 임시로 묶어두는 작은 그룹.
   • 예를 들어, 과일처럼 보이는 데이터들을 모아두는 것.
2. 나중에 더 세분화: 이렇게 대략적으로 묶어둔 데이터를 나중에 시간이 있거나 필요할 때, 더 세밀하게 분류해서 사과, 바나나, 오렌지처럼 정확한 그룹으로 나누는 작업을 할 수 있다.

이러한 문제를 해결하기 위해 우리는 데이터 스트림의 거칠게(granular) 표현된 구조를 나타내기 위해 Granular-Ball 구조를 사용한다. 이 구조는 온라인과 오프라인 단계에서 모든 데이터 포인트에 대한 계산을 제거한다. 또한, 우리는 Granular-Ball 구조에 퍼지(fuzziness) 개념을 도입하여 개념 변화로 인한 클러스터 경계 겹침 문제를 해결한다. 실험 결과, 합성 및 실제 데이터셋에서 우리의 접근법이 기존 데이터 스트림 클러스터링 알고리즘에 비해 효율적이고 정확한 클러스터링 성능을 달성한다는 것이 입증되었다.

 

I. INTRODUCTION

데이터 스트림이란, 다양한 분야에서 매일 매우 빠른 속도로 생성되는 시간 연속적인 데이터를 의미한다. 예를 들어, 센서 네트워크에서의 데이터 마이닝, 기상 분석, 소셜 네트워크에서의 커뮤니티 추적 등이 데이터 스트림의 대표적인 응용 사례이다. 이러한 데이터 스트림에서 유용한 정보를 추출하는 것은 상당히 중요한 과제이다.

최근 들어 데이터 스트림을 클러스터링하기 위한 알고리즘들이 많이 제안되고 있다. 두 가지 주요 방법은 마이크로 클러스터 기반과 비 마이크로 클러스터 기반 방식이다

• 마이크로 클러스터 기반 알고리즘은 들어오는 데이터를 작고 유사한 그룹으로 묶어서 정보를 축적한다.
• 반면에 비 마이크로 클러스터 기반 알고리즘은 데이터 공간을 그리드(격자)처럼 분할하고, 각 영역에 들어오는 데이터를 쌓아두는 방식이다.

데이터 스트림 클러스터링 알고리즘은 주로 온라인 또는 온라인-오프라인 단계로 나뉜다.

• 온라인 단계에서는 새로운 데이터가 나타날 때마다 바로 클러스터링을 업데이트하고, 데이터를 오래된 순서로 '감쇠(오래된 데이터를 덜 중요하게 만드는)' 처리를 한다.

온라인-오프라인 단계에서는 알고리즘이 새로운 데이터와 마이크로 클러스터 구조를 계산하고 관련된 마이크로 클러스터에 합병한다.

 

기존의 데이터 스트림 클러스터링 알고리즘들은 온라인 또는 온라인-오프라인 프레임워크에 기반을 두고 있다. 많은 방법들이 온라인 단계에서 마이크로 클러스터들을 업데이트하기 위해 정밀한(fine-grained) 접근 방식을 사용한다. 그림 1(a)에 나타난 바와 같이, 새로운 샘플에 대한 정밀한 할당 과정이 묘사되어 있으며, 빨간색 점은 새로 도착한 샘플을 나타내고, 다른 색상으로 표시된 점의 집합은 서로 다른 마이크로 클러스터를 나타낸다.

새로운 샘플이 도착하면, 알고리즘은 각 샘플을 스캔하고, 기존의 마이크로 클러스터 구조 또는 파티션과의 관계를 계산한 후, 샘플을 해당하는 마이크로 클러스터나 파티션에 병합해야 한다. 만약 기존 구조에 병합될 수 없으면, 새로운 파티션이나 마이크로 클러스터가 별도로 생성된다. 이러한 정밀한(fine-grained) 접근 방식은 비효율적인 알고리즘으로 이어진다.

반면에, 그림 1(b)에 표시된 것처럼, 검은 원 안에 포함된 샘플들을 할당의 단위로 간주하여, 그룹 단위로 샘플을 한꺼번에 할당하는 방식을 사용할 수 있으며, 이는 대략적인(coarse-grained) 접근 방식이다.

또한, 데이터의 지속적인 유입과 변화하는 특성을 처리하고, 현재 클러스터링에 대한 과거 데이터의 영향을 제거하기 위해, 데이터 스트림 클러스터링 알고리즘은 슬라이딩 윈도우(sliding window), 감쇠 윈도우(damped window), 랜드마크 윈도우(landmark window) 등의 다양한 윈도우 모델을 사용한다.

감쇠 윈도우 모델을 사용하는 알고리즘에서는, 각 객체의 감쇠율을 통계적으로 평가하여 파티션 내에서 전체 감쇠율을 종합적으로 계산한다. 또는, 파티션에 대해 감쇠 값을 직접 설정하여 모든 객체를 스캔하지 않고도 전체 감쇠를 수행할 수 있다. 이러한 처리 방법들은 감쇠 정확도와 효율성 사이의 균형을 보장하지 않는다.

끊임없이 변화하는 스트리밍 환경에서, 클러스터는 개념 변화로 인해 병합 또는 분할 현상을 겪을 수 있다. 이 과정은 클러스터 경계의 겹침으로 이어져 최종 클러스터링 결과에 영향을 미칠 수 있다. 따라서, 우리는 데이터 스트림 클러스터링 알고리즘에 대한 조사를 수행하였다.

우리는 퍼지 개념을 도입하는 것이 이 문제를 완화할 수 있음을 발견하였다. 예를 들어, FuzzStream은 데이터 스트림 클러스터링 알고리즘에 퍼지를 처음 도입한 알고리즘이고, d-FuzzStream은 FuzzStream을 기반으로 제안되었으며, TSFDBSCAN은 최근에 제안된 알고리즘이다.

또한, 데이터 스트림 시나리오에서는 클러스터의 모양과 수가 시간이 지남에 따라 변하기 때문에, 올바른 클러스터링이 데이터 스트림 클러스터링 알고리즘의 이상적인 기능이다.

Density Peak Clustering (DPC) [18]는 비구형(non-spherical) 클러스터를 식별할 수 있으며, 클러스터의 개수를 사전에 지정할 필요가 없는 밀도 기반 클러스터링 알고리즘이다. 그러나 새로운 데이터가 지속적으로 도착함에 따라, 클러스터 간의 데이터 밀도의 큰 차이와 개념 변화로 인해 발생하는 클러스터 경계의 겹침은 DPC가 최적의 클러스터링 결과를 생성하지 못하게 만들 수 있다.

 

- 비구형 클러스터란?

일반적인 클러스터링 알고리즘은 데이터를 둥근 형태로 묶으려는 경향이 있다. 그러나 현실에서 데이터는 구형이 아니고 타원형이나 복잡한 형태로 나타날 수 있다. 비구형 클러스터는 바로 이런 둥글지 않은 모양의 클러스터를 말하며, 이를 잘 찾아내는 알고리즘이 필요하다.

- 클러스터 개수를 사전에 지정할 필요가 없다?

일반적인 클러스터링 알고리즘(예: K-평균)에서는 클러스터의 개수를 미리 정해야 한다. 즉, 데이터를 몇 개의 그룹으로 나눌지 사전에 지정해야 한다. 하지만, 실제 데이터에서는 클러스터가 몇 개인지 모르는 경우가 많다. DPC(Density Peak Clustering)는 클러스터 개수를 미리 설정하지 않아도 된다. 이 알고리즘은 데이터의 밀도를 기준으로 클러스터를 자동으로 생성하기 때문이다.

- DPC가 클러스터를 생성하는 방식

DPC 알고리즘은 데이터의 밀집 정도를 기준으로 클러스터를 나눈다. 밀도가 높은 부분을 클러스터의 중심으로 보고, 그 중심 주변 데이터를 하나의 클러스터로 묶는다. 즉, 데이터가 많이 모여 있는 부분을 클러스터로 구분하는 방식이다. 예를 들어, 데이터가 두 군데에 밀집되어 있다면 2개의 클러스터가, 세 군데에 모여 있다면 3개의 클러스터가 자동으로 만들어진다.

- DPC의 문제점

그러나 새로운 데이터가 계속 유입되거나, 클러스터 간 데이터 밀도의 차이가 크다면 DPC는 최적의 클러스터링 결과를 내지 못할 수 있다. 또한, 개념 변화로 인해 클러스터 경계가 겹칠 수 있다. 개념 변화란 시간이 지나면서 데이터의 특성이 바뀌는 현상이다. 이러한 변화는 클러스터 경계를 애매하게 만들어, 데이터가 정확하게 분류되지 않을 수 있다.

이 문제를 해결하기 위해 우리는 GB-FuzzyStream이라고 불리는 효과적인 데이터 스트림 퍼지 클러스터링 방법을 설계하였다. 우리는 데이터 스트림의 대략적인 표현을 제공하기 위해 그라뉼-볼 구조를 사용한다. 추가적으로, 우리는 그라뉼-볼 구조에 퍼지 개념을 도입하여 두 가지 구조, 즉 퍼지 그라뉼-볼(FGB)과 퍼지 마이크로볼(FMB)을 생성한다. 

GB-FuzzyStream은 초기 데이터를 사용하여 FMB를 생성하는데, 이는 다른 알고리즘의 마이크로 클러스터 구조와 유사하다.

새로운 입력 데이터가 도착하면, 알고리즘은 새로운 샘플을 사용하여 FGB를 생성 -> 이를 FMB에 병합-> FMB에 감쇠(decay) 처리

FGB와 FMB를 생성하는 과정에서 우리는 샘플이 서로 다른 볼(ball)에 속하는 소속도(membership)에 따라 겹치는 영역의 데이터를 분할한다. 이 방법은 개념 변화로 인한 클러스터 경계 겹침 문제를 효과적으로 해결한다.

더 자세히 알아보자.

 

1. 클러스터 경계 겹침 문제를 해결하는 방법

먼저, 클러스터 경계 겹침 문제란, 데이터가 여러 클러스터의 경계에 걸쳐있어서 어느 클러스터에 속해야 할지 애매한 상황을 말한다. 특히, concept drift가 발생하면, 데이터의 특성이 바뀌면서 이런 문제가 더 자주 발생한다. 

이 문제를 해결하기 위해 GB-FuzzyStream에서는 퍼지 그라뉼-볼(FGB)과 퍼지 마이크로볼(FMB)을 사용한다. 퍼지 클러스터링은 데이터를 여러 클러스터에 동시에 속할 수 있는 방식으로 처리한다. 즉, 한 데이터가 어느 정도는 클러스터 A에, 또 어느 정도는 클러스터 B에 속한다고 할 수 있다. 이런 방식으로, 데이터가 경계에 걸쳐 있어도 무리하게 하나의 클러스터에만 속하게 하지 않고, 퍼지 소속도를 계산해 유연하게 처리한다.

결국, 이 퍼지 방식 덕분에 클러스터 경계 겹침 문제를 효과적으로 해결할 수 있다. 데이터가 애매하게 여러 클러스터에 속할 때, 퍼지 소속도를 통해 그 애매함을 자연스럽게 처리하는 것이다.

2. 서로 다른 클러스터 간 밀도 차이 문제를 완화하는 방법

데이터 밀도가 높으면 그 주위에 데이터가 많이 몰려있다는 뜻이고, 밀도가 낮으면 데이터가 흩어져 있다는 의미이다. 이때 클러스터 간 밀도 차이가 심하면 DPC 알고리즘에서 문제가 발생할 수 있다. DPC는 밀도가 높은 부분을 클러스터 중심으로 잡기 때문에, 클러스터 간 밀도 차이가 크면 제대로 클러스터링을 못 할 수 있다.

GB-FuzzyStream은 이 문제를 해결하기 위해 FMB의 중심을 DPC 알고리즘에 입력으로 사용한다. FMB에서 미리 데이터를 조정해 서로 다른 클러스터의 밀도 차이를 줄여준다. 그 후에 DPC를 적용하면, 서로 다른 클러스터 간 밀도 차이 문제가 완화되고 더 정확한 클러스터링이 가능해진다.

즉, GB-FuzzyStream이 데이터를 먼저 잘 다듬어준 덕분에 DPC가 밀도 차이 문제를 덜 겪고, 클러스터링 성능이 더 좋아진다는 것이다.

 

II. RELATED WORK

기존의 데이터 스트림 클러스터링 알고리즘 분류 : 파티션 기반 알고리즘, 밀도 기반 알고리즘, 그리드 기반 클러스터링 알고리즘

데이터 스트림 클러스터링 알고리즘의 특징(퍼지 여부 포함)은 표 I에 나와 있다. TSF-DBSCAN과 d-FuzzStream을 제외한 나머지 알고리즘들은 개념 변화로 인한 클러스터 경계 겹침 문제를 처리하지 못하며, 이는 클러스터링 결과에 부정적인 영향을 미칠 수 있다. GB-FuzzyStream은 데이터 처리에서 대략적인(coarse-grained) 접근 방식을 사용하고, 퍼지를 도입하여 클러스터 경계 겹침 문제를 해결한다.

A. 데이터 스트림 클러스터링

CluStream 은 BIRCH 알고리즘의 CF 벡터를 확장한 클래식한 두 단계 스트림 클러스터링 알고리즘이다. CluStream은 K-평균 알고리즘을 기반으로 분할-정복 전략을 사용하여 데이터를 클러스터링하고, 적은 메모리 공간에서 상수 요소를 가진 대략적인 결과를 달성한다. CluStream은 피라미드 시간 프레임을 사용하여 데이터 스트림의 진화를 기록하지만, 역사적 데이터의 감쇠 문제를 고려하지 않기 때문에 최신 데이터의 중요성을 반영하지 못한다. 또한, 클러스터의 개수를 미리 지정해야 하며, 비구형 클러스터를 효과적으로 처리하지 못한다.

DenStream 은 밀도 기반 클러스터링 개념과 마이크로 클러스터를 결합한 알고리즘이다.

온라인 단계 : 두 가지 유형의 마이크로 클러스터, 즉 잠재적 핵심 마이크로 클러스터(p-mc)와 이상치 마이크로 클러스터(o-mc)를 정의한다. DenStream은 각 마이크로 클러스터 구조에 시간 가중치를 할당하고, 감쇠를 위한 감쇠 윈도우 모델을 사용한다. 새로운 데이터 포인트가 도착하면, DenStream은 업데이트된 반경을 기반으로 해당 데이터 포인트를 가장 가까운 p-mc에 삽입한다. 삽입이 실패하면, 가장 가까운 o-mc에 삽입하려고 시도한다.

오프라인 단계 : 밀도 도달 가능성 및 밀도 연결성을 기반으로 최종 클러스터링 결과를 결정하기 위해 마이크로 클러스터를 사용한다. 이 알고리즘은 밀도 기반이기 때문에 클러스터의 형태와 밀도에 대한 요구가 높다.

D-Stream은 데이터 공간을 다차원 그리드로 분할하여 대규모 데이터 스트림을 병렬 처리하고 클러스터링한다.

온라인 단계 : 초기 그리드 분할을 기반으로 클러스터를 생성하고, 그리드에 감쇠 계수를 정의한다. 새로운 데이터 포인트가 도착하면, 그리드 셀 중 가장 가까운 셀에 할당한다.

오프라인 단계 : 그리드 밀도를 계산하고, 그리드의 밀도를 기반으로 클러스터링을 수행한다. 이 알고리즘은 시간 범위, 감쇠 계수, 데이터 밀도 간의 관계를 고려하여 고품질의 클러스터를 생성하지만, 적절한 그리드 분할과 병합 임계값 선택에 어려움이 있다.

MuDi-Stream은 다중 밀도 환경에서 데이터 스트림 클러스터를 발견하는 방법이다. 온라인 단계에서는 계속해서 변화하는 데이터 스트림을 핵심 마이크로 클러스터 형태로 요약하여 유지한다. 또한, 이상치에 의한 노이즈 문제를 처리하기 위해 그리드 기반 접근 방식을 사용한다. 이를 바탕으로 MuDi-Stream은 핵심 마이크로 클러스터와 그리드의 가중치에 기반한 새로운 가지치기(pruning) 전략을 도입하여 실제 이상치를 식별하도록 한다. 오프라인 단계에서는 DBSCAN의 변형을 사용하여 마이크로 클러스터를 클러스터링한다. 그러나 MuDi-Stream은 그리드에 대한 시간 감쇠를 정확하게 정의하지 못하며, 이전 데이터를 전체적으로 취급하고 수정된 감쇠 윈도우를 사용하여 감쇠를 처리한다.

CEDAS [31] 알고리즘은 온라인 데이터 스트림 클러스터링 방법이다. 각 마이크로 클러스터는 반지름이 r/2와 r 사이인 껍질 영역(shell region)과 반지름이 r/2 이하인 핵심 영역(core region)으로 구성된다. 새로운 데이터가 도착하면, 해당 데이터 샘플이 현재 마이크로 클러스터 내에 있는지 확인하여 마이크로 클러스터의 에너지를 1로 리셋한다. 그 샘플이 핵심 영역에 있는지 껍질 영역에 있는지 추가로 확인한다. 만약 샘플이 껍질 영역에 있다면, 마이크로 클러스터의 중심을 껍질에 있는 샘플의 평균으로 재귀적으로 업데이트한다. 마지막으로, 마이크로 클러스터의 지역 밀도가 임계값을 초과하면 클러스터의 일부로 간주한다. 알고리즘은 마이크로 클러스터의 핵심 영역과 교차하는 다른 마이크로 클러스터가 있는지 계속해서 탐색하며, 찾게 되면 동일한 클러스터에 할당한다. MuDi-Stream과 유사하게, CEDAS는 마이크로 클러스터 감쇠율을 계산하는 데 있어 정밀성이 부족하다.

 

B. 데이터 스트림 퍼지 클러스터링

FuzzStream은 데이터 스트림 클러스터링에 퍼지 개념을 도입한 최초의 알고리즘이다. 이를 기반으로, 저자들은 d-FuzzStream 알고리즘을 제안하였다.

온라인 단계 : d-FuzzStream은 데이터를 퍼지 마이크로 클러스터(FM iC)라고 불리는 클러스터 특징 집합으로 요약한다. 동시에 d-FuzzStream은 FM iC의 개수에 대한 상한선을 설정한다. 만약 기존 FM iC의 개수가 상한선에 도달하면, 알고리즘은 가장 오래된 퍼지 마이크로 클러스터를 제거 -> 새로운 데이터를 위한 새로운 FM iC를 생성

오프라인 단계 : WFCM을 사용하여 이 FM iC들을 클러스터링한다. 그러나 d-FuzzStream의 온라인 요약 과정은 비효율적이며, 클러스터의 개수를 사전에 입력해야 하기 때문에 지속적으로 변화하는 데이터 스트림 환경에 적응하기 어렵다.

최근 제안된 TSF-DBSCAN은 DBSCAN의 세 가지 확장을 통해 퍼지 경계 확장을 도입하였다. TSF-DBSCAN은 핵심 영역과 껍질 영역으로 이루어진 마이크로 클러스터를 정의한다. 껍질 영역의 샘플 포인트가 핵심 영역에 속하는 소속도는 그 거리에 반비례한다.

온라인 단계에서는 새로운 샘플이 다른 포인트의 핵심 및 껍질 영역에 추가된다.

오프라인 단계에서는 알고리즘이 감쇠 윈도우를 적용하여 핵심 및 껍질 영역의 샘플을 감쇠시키고, 만료된 샘플을 제거한다. 그 후 샘플의 핵심 영역에 대한 가중치를 기반으로 해당 샘플이 핵심 객체인지 여부를 결정한다. 핵심 객체의 핵심 및 껍질 영역을 하나의 클러스터로 처리한다. 마지막으로, 알고리즘은 클러스터를 확장하기 위해 핵심 영역의 핵심 객체를 계산한다. TSF-DBSCAN은 퍼지 경계 확장을 도입하여 클러스터 경계 겹침 문제를 효과적으로 해결하였다. 그러나 TSF-DBSCAN은 마이크로 클러스터를 업데이트하고 클러스터를 확장할 때 각 샘플을 반복적으로 스캔해야 하기 때문에 알고리즘의 효율성이 낮다.

 

C. 대략적인(coarse-grained) 방법

Chen Lin이 Science에 발표한 연구에 따르면, 인간 인지는 넓은 범위의 우선순위 특성을 보인다고 한다 [33]. 그라뉼 컴퓨팅(granular computing)이라는 개념은 제어 이론의 유명한 전문가인 Zadeh에 의해 제안되었으며, 이러한 인지적 특성에 기반을 둔다 [34]. 그라뉼 컴퓨팅에서는 그라뉼의 크기가 증가할수록 효율성과 노이즈에 대한 강인함이 증가한다. 그러나, 기존의 인공지능 알고리즘들은 주로 매우 세밀한 수준(예: 개별 데이터 포인트나 픽셀)에서 작동하며, 더 대략적인 수준의 표현을 제공하지 않는다. 이는 비효율성과 노이즈에 대한 취약함을 초래한다.

이 문제를 해결하기 위해, Wang Guoyin, Xia Shuyin 등의 연구자들은 **다중 그라뉼 인지 학습(multi-granularity cognitive learning)**에서 영감을 받아 그라뉼-볼(granular-ball) 컴퓨팅 모델을 도입하였다 [35], [36]. 이 접근법은 '그라뉼-볼'을 사용하여 샘플 공간을 덮거나 일부를 덮고, 이를 학습 방법의 입력으로 사용한다. 이를 통해 다중 그라뉼 학습 속성과 샘플 공간의 정확한 특성을 표현할 수 있게 된다. 그라뉼-볼 구조는 샘플 공간을 잘 덮거나 부분적으로 덮으며, 하나의 그라뉼-볼 구조는 여러 샘플을 포함하여 대략적인 표현을 제공한다.

우리 알고리즘의 흐름에서, GB-FuzzyStream은 새로 들어온 데이터를 사용하여 퍼지 그라뉼-볼(fuzzy granular-balls)을 생성하고, 초기 데이터를 사용하여 마이크로 클러스터와 유사한 퍼지 마이크로볼(fuzzy micro-ball) 구조를 만든다. 이후 이 퍼지 그라뉼-볼을 하나의 단위로 퍼지 마이크로볼에 병합하여, 퍼지 마이크로볼을 업데이트하는 작업을 완료한다. 마지막으로, 오프라인 클러스터링에서 우리는 퍼지 마이크로볼의 중심을 클러스터링 알고리즘의 입력으로 사용한다.

III. THE PROPOSED METHOD

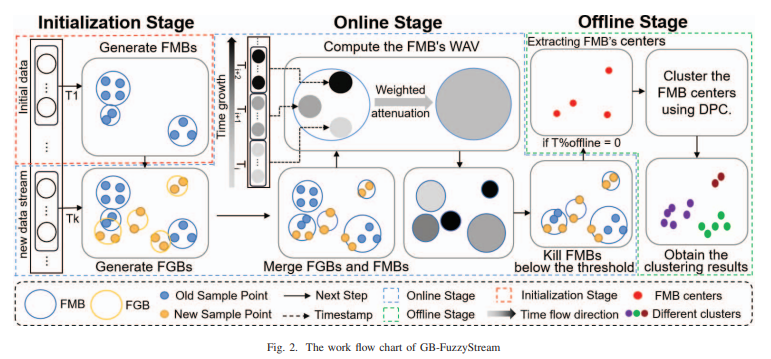
그림 2에서 설명된 것처럼, 우리의 알고리즘은 세 가지 구별된 단계로 구성된다.

 

• 초기화 단계 (Initialization Stage):
  • 초기 데이터가 들어오면 먼저 FMB가 생성된다. 초기 데이터로 FMB를 만든 후, 새로운 데이터 스트림이 들어오면 그때 FGB가 생성된다.
  • 즉, 초기화 단계에서 먼저 FMB를 만들고, 새로운 데이터가 실시간으로 들어올 때는 그 데이터를 FGB로 처리하는 거야.,
• 온라인 단계 (Online Stage):
  • FGB와 FMB의 결합: 실시간으로 새로 들어오는 데이터를 사용해서 FGB를 생성하고, 이 FGB는 기존의 FMB에 결합된다. 그래서 온라인 단계에서는 FGB와 FMB가 병합된다.
  • 가중치 감쇠(Weighted Attenuation): FMB는 새로운 데이터를 병합하면서 가중치를 업데이트하고, 오래된 FMB는 일정 임계값(Threshold) 이하로 가중치가 떨어지면 제거된다.
• 오프라인 단계 (Offline Stage):
  • FMB의 중심을 클러스터링 알고리즘의 입력으로 사용: 오프라인 단계에서 FMB의 중심을 추출해 DPC(Density Peak Clustering) 알고리즘에 넣어 클러스터링을 수행한다.
  • 최종 클러스터링 결과를 얻는다.

 

이 논문은 다음과 같은 이유로 새로운 데이터 스트림 퍼지 클러스터링 알고리즘을 제안한다:

1. 기존의 두 단계 알고리즘은 개별 단계의 효율성을 최적화하는 데 초점을 맞추지만, 두 단계 모두에 대한 전체적인 최적화 접근 방식이 부족하다.
2. 개념 변화(Concept drift) 현상은 마이크로 클러스터 간 경계가 겹치는 문제를 초래할 수 있다. 기존의 알고리즘은 이러한 겹치는 영역에 있는 샘플을 정확하게 할당하지 못하며, 이는 이후의 클러스터링 결과에 영향을 미친다.
3. 기존 알고리즘들은 마이크로 클러스터의 감쇠 수준을 계산할 때 효율성과 정확성 간의 균형을 맞추지 못한다.

GB-FuzzyStream의 매개변수 설명과 값은 표 II에 나와 있다. ρ∗와 δ∗는 DPC에서 가져온 매개변수로, 값은 0.5로 설정된다. m과 eps는 FCM에서 가져온 매개변수로, 각각 2와 10으로 설정된다. 우리는 FMB의 감쇠율을 λ와 임계값을 조정하여 제어한다.

 

정의 1: 퍼지 그라뉼볼(Fuzzy Granular-Ball, FGB):

FGB는 새로 들어온 데이터를 임시로 저장하는 구조이며, 이후 퍼지 마이크로볼(FMB)로 병합된다. FGB는 FMB를 생성하는 기초가 되며, 중심 ci는 그라뉼볼 내 모든 샘플 포인트의 평균이다. 반경 ri는 그라뉼볼 내에서 중심 ci와 가장 먼 점 pk​ 간의 최대 거리로 정의된다. 수식은 다음과 같다.

정의 2: 퍼지 마이크로볼(Fuzzy Micro-Ball, FMB):

FMB는 오프라인 단계에서 FMB를 기반으로 클러스터를 생성하는 마이크로 클러스터 구조이다. FMB 구조에는 중심 **cic_ici​**와 반경 ri뿐만 아니라 DMi, WAV, 샘플 포인트 개수 nfmb, 그리고 사전(dictionary) 구조가 포함된다.

클러스터 경계 겹침 문제를 해결하기 위해, 우리는 퍼지 C-평균(Fuzzy C-Means, FCM) [37]을 FGB 또는 FMB의 분할 과정에 도입하고, 초기 반복 중심을 선택하기 위한 결정적 방법인 Ball-Tree를 고안하였다. 그림 3(a)에서 보여지듯이, 우리는 먼저 볼 내부의 모든 샘플의 중심 O를 계산한다. 그런 다음, O에서 가장 먼 지점 p1을 찾고, p1에서 가장 먼 지점 p2를 계산한다. 마지막으로 O와 p1 사이의 중점 O1과 O와 p2 사이의 중점 O2를 계산한다. 이를 통해 초기 반복 중심 O1과 O2를 얻을 수 있다.

정의 3: (UBallij , Oi) :

UBallij​는 볼 내부의 i번째 반복 중심 Oi에 대한 j번째 샘플의 소속도를 나타낸다.

여기서 ∥⋅∥는 2-노름을 나타내며, N은 FMB 또는 FGB에 있는 샘플 수를 나타낸다. m은 퍼지 지수를 의미하며, pj는 FMB 또는 FGB 안에 있는 샘플 포인트이다.

 

Lemma 1: 데이터 집합 D와 할당된 데이터 포인트 pj∈ball이 주어졌을 때, FCM의 목적 함수를 기반으로 한 볼 분할의 목적 함수는 다음과 같다.

 

레마 1에서 볼 수 있듯이, FCM에 기반한 볼 분할 과정은 수렴성을 가진다. UBall과 O에 대해 안정성이 확보되면, 그림 3(b)-(c)에 표시된 것처럼 소속 행렬(UBall)을 기반으로 데이터를 분할하여 두 개의 자식 볼(child-balls)을 생성한다.

 

Proof 1: I 번째 iteration 후를 추정할때, 목적 함수는 J(I)이며, I+1번째 반복 후의 목적 함수 값은 J(I + 1)이다. 식 3과 식 4의 업데이트 규칙에 따라, 다음과 같은 결과를 얻을 수 있다:

중간에 오타는 J(I) - J(I +1) >= 0 이다.

레마 1에서 볼 수 있듯이, FCM에 기반한 볼 분할 과정은 수렴성을 가진다. UBall과 O에 대한 안정성이 확보되면, **그림 3(b)-(c)**에 표시된 것처럼 소속 행렬 UBall을 기반으로 데이터를 분할하여 두 개의 자식 볼(child-balls)을 생성한다.

DMweight는 볼을 분할할지를 평가하는 중요한 기준으로 작용한다. 자식 볼들의 DMweight가 부모 볼의 DM보다 클 경우, 부모 볼은 분할될 수 있다.

 

정의 4 : 가중 분포 측정치(Weighted Distributed Measure, DMweight)

DMi는 FMB 또는 FGB 내의 모든 포인트 p_j가 중심 c_i에 얼마나 가까운지를 나타내는 평균값이다. 계산 공식은 다음과 같다: DMi값이 클수록 포인트들이 뭉쳐있다고 생각하면 됨.

여기서 N_i는 볼 내의 포인트 개수를 나타내며, DM_1과 DM_2는 각각 두 자식 볼의 DM 값을 나타낸다. N은 부모 볼(FMB 또는 FGB) 내의 전체 포인트 개수이다. 그림 3(c)-(d)에서 보듯이, 지정된 분할 기준이 충족되면 볼은 더 이상 분할할 수 없을 때까지 계속 나누어진다.

1. 볼(fmb 또는 fgb)을 입력으로 받는다.
2. m = 2, eps = 10, Uorigin = [0], V = [O1, O2]로 초기화한다.
3. 식 3을 사용해 UBall을 초기화한다.
4. UBall과 Uorigin의 차이가 eps보다 작아질 때까지 반복한다.
5. Uorigin을 UBall로 업데이트하고, 식 4를 통해 V = [O1, O2]를 업데이트한 다음 UBall을 식 3을 통해 다시 업데이트한다.
6. 반복이 끝나면, UBall에 따라 볼을 ball1과 ball2로 분할한다.
7. 만약 볼이 fmb라면, 각 키 tkey에 대해 데이터를 기록한다.
8. tkey에 속한 데이터를 fmb1과 fmb2에 나누어 기록하고, fmb1.map[tkey]과 fmb2.map[tkey]에 저장한다.
9. 분할 결과를 Balls에 추가한다.

A. FGB와 FMB의 생성 및 분할

알고리즘 1은 FGB 또는 FMB를 두 개로 분할하는 과정을 설명한다. 먼저, 필요한 매개변수를 초기화한다. 식 3에 따라 **소속도 행렬(UBall)**을 계산한다. 그 후, FCM(Fuzzy C-Means) 알고리즘과 유사하게, V와 UBall을 반복적으로 업데이트하여 종료 조건이 충족될 때까지 반복한다. 마지막으로, UBall에 기반해 현재 데이터를 두 개의 자식 볼(child-balls)로 분할한다.

알고리즘 2: 퍼지 그라뉼볼(Fuzzy Granular-Balls)의 생성

1. 데이터셋 D를 fgb로 처리하고 이를 FGBs에 추가한다.
2. FGBs에 있는 각 fgb에 대해:
3. 알고리즘 1을 통해 fgb를 fgb1과 fgb2로 분할한다.
4. 식 7부터 식 9까지 사용해 DM과 DMweight를 계산한다.
5. DMweight가 DM보다 크면, fgb1과 fgb2를 FGBs에 추가하고, 현재 fgb는 제거한다. -> 분할 후 자식볼들이 부모볼에 비해 더 밀집되었다는 뜻. 성공적인 분할이었다는 뜻!
6. 남아있는 FGBs를 계속 스캔하거나 새롭게 추가된 FGB들을 확인한다.
7. 모든 FGB가 분할되지 않은 상태가 되면, FGB의 평균 반경과 중간값 반경을 계산하여 R을 구하고, 1.5배 큰 값을 기준으로 너무 큰 FGB를 확인한 후 이를 분할한다.

FGB는 FMB를 만드는 기반이며, 그 생성 과정은 알고리즘 2에서 설명된다.

 

결국 먼저 초기로 FMB로 구조를 설정해놓고 온라인 단계에서 새로운 데이터가 들어오면, 이를 임시로 FGB(Fuzzy Granular-Ball) 형태로 저장한다. FGB는 새로운 데이터 포인트의 집합을 나타내며, 임시적인 클러스터링 단위로 사용된다. 그후에 생성된 FGB는 기존의 FMB와 병합을 시도한다. 만약 병합 조건(예: 거리 또는 밀도 조건)을 만족하면, FGB의 데이터를 기존 FMB에 추가하여 갱신한다. 병합이 불가능할 경우, FGB 자체를 새로운 FMB로 변환하여 FMB 집합에 추가한다.

 

 

GB-FuzzyStream은 개념 변화(concept drift)로 인한 클러스터 경계 겹침 문제를 완화하기 위해, 샘플 포인트가 경계에 겹칠 경우 소속도에 따라 해당 FMB로 나눈다.

 

• 소속도는 각 FMB에 데이터를 나눌 때 가중치로 활용됩니다. 예를 들어, FMB1에 대한 소속도가 0.7이고, FMB2에 대한 소속도가 0.3이면, 이 데이터 포인트는 FMB1에 70%, FMB2에 30% 정도 속한다고 해석합니다.
• 이러한 방식을 통해 데이터 포인트가 여러 클러스터에 걸쳐 분포할 수 있으며, 경계 겹침 문제를 완화할 수 있습니다.

 

최종 클러스터링 과정에서, 클러스터링은 각 FMB에 대해 수행되며, 겹치는 샘플을 다시 분할할 필요가 없다. 이 방식은 효율성을 높이는 동시에 클러스터 경계 겹침 문제를 완화한다.

 

B. 초기화 단계

마이크로 클러스터가 두 개의 다른 시간 T1과 T2에서 각각 n1과 n2개의 데이터 포인트로 구성되었다고 가정하자. 전통적인 감쇠 방법은 모든 n1 + n2 샘플을 스캔하고, 감쇠 함수로 각 샘플의 감쇠 정도를 업데이트하며, 샘플을 제거할지 결정한다. 또는, 전체 마이크로 클러스터를 하나의 단위로 간주해, 감쇠 함수를 사용해 전체 클러스터에 감쇠를 적용할 수 있다. 그러나 이러한 방법들은 감쇠 정확성과 효율성 간의 균형을 맞추지 못한다.

이를 해결하기 위해, 우리는 감쇠 과정을 최적화하기 위해 사전(dictionary) 구조를 설계하였다. FMB를 계산할 때, T1이나 T2에서 온 데이터가 있더라도 그들의 감쇠 정도는 일관된다. 우리는 각 시간에 대해 감쇠 함수를 사용해 F(T1)과 F(T2)를 계산하고, FMB의 감쇠 정도는 가중 평균으로 계산된다:

사전은 시간 T와 해당 샘플 개수 n을 키-값 쌍으로 저장한다. 이 접근 방식으로, 우리는 맵을 한 번만 스캔하여 FMB의 감쇠 정도를 계산할 수 있다. 시간이 지나면서 FMB 내 대부분의 샘플이 큰 감쇠를 보이고, 새로 들어온 샘플이 적으며, FMB의 WAV가 임계값보다 낮으면, 전체 FMB를 삭제한다.

정의 5: 가중 감쇠 값 (Weighted Attenuation Value, WAV)

현재 시간이 T이고, 감쇠 계수(λ)가 있을 때, 시간 Ti에 도착한 데이터 포인트 p의 감쇠 정도는 다음과 같이 계산된다:

FMB가 서로 다른 k개의 시간에서 온 데이터로 구성되어 있다고 가정하면, 사전 맵은 Ti를 키로, 해당 시간에 병합된 데이터 포인트 수 ni를 값으로 저장한다. FMB의 WAV 계산은 다음과 같다:

여기서 n_fmb는 FMB 내의 데이터 포인트 수를 의미한다. 부모 볼의 사전은 나누어져야 하며, 자식 볼의 사전은 각 타임스탬프에서의 데이터 포인트 수를 기록해야 한다.

 

 

1. 알고리즘 2에 따라 D를 사용하여 FGB들을 생성한다.
2. FGBs에 있는 각 fgb에 대해 다음 단계를 수행한다.
3. fgb에 있는 데이터 포인트의 수를 계산하여 nfgb로 저장한다.
4. 중심 c, 반지름 r, DM(밀도 측정치), WAV(가중 감쇠 값)을 식 1, 식 2, 식 8, 식 11을 이용해 계산한다.
5. 퍼지 마이크로 볼 구조를 생성한다. 여기에는 다음과 같은 요소들이 포함된다:
   • FMB(WAV) = 1 (가중 감쇠 값)
   • FMB(DM) = DM (밀도 측정치)
   • FMB(center) = c (중심)
   • FMB(num) = nfgb (데이터 포인트 수)
   • FMB(radius) = r (반지름)
   • FMB(map) = {T : nfgb} (사전 형태로 타임스탬프와 데이터 포인트 수를 기록)
   1. FMB를 FMBs에 추가한다.

• 모든 fgb에 대해 위 단계를 반복한다.
• 초기화 단계에서는 알고리즘 2를 통해 초기 데이터로부터 FGB 집합을 생성한 후, 각 FGB에 대해 nfgb, 중심, 반지름, DM, WAV 등의 메트릭을 계산하여 FMB를 생성하고 이를 FMBs에 추가한다. 마지막에는 FMB 집합이 완성된다.

C. 온라인 단계

• 온라인 단계에서는 새롭게 들어오는 데이터가 여러 개의 FGB를 생성하게 된다.
• FGB를 FMB와 병합한 후 너무 커지지 않도록 하기 위해, MIR (Maximum Impact Range) 개념을 도입하여 FGB가 가장 가까운 FMB와 병합할 수 있는지를 판단한다.
• 만약 FGB가 기존의 FMB와 병합할 수 없다면, FGB 데이터를 사용하여 새로운 FMB를 생성하게 된다.

 

정의 6: 최대 영향 범위 (Maximum Impact Range, MIR)

MIR는 FGBi가 가장 가까운 FMBj와 병합될 수 있는지 여부를 결정하는 기준이다. MIR는 다음과 같이 정의된다:

여기서 dist()는 두 볼의 중심 간의 거리를 나타내고, R_{fgbi}는 FGBi의 반경을 의미한다. FGBi는 병합하려는 볼이고, FMBj는 FGBi와 가장 가까운 볼이다. FMBk는 FMBj와 가장 가까운 볼이다. MIR = 1이면 FGBi가 FMBj와 병합될 수 있고, MIR = 0이면 병합이 불가능하다.

그림 4에서 설명한 것처럼, FGB1은 FMB11과 병합될 수 있다. 왜냐하면 FGB1과 FMB11 사이의 거리와 FGB1의 반경을 더한 값이 FMB11과 FMB12 사이의 거리보다 작기 때문이다. 이로 인해 MIR은 1이 된다. 반면에 FGB2는 MIR 조건을 만족하지 않기 때문에 병합될 수 없다. 따라서 FGB2의 데이터를 사용해 새로운 FMB2를 생성한다.

초기화가 완료되면, 우리는 FMB들의 집합을 얻게 된다. 알고리즘 4에서 설명한 바와 같이, 온라인 단계 동안 각 타임스탬프에서 새로 들어오는 데이터는 알고리즘 2를 통해 처리되어 해당하는 FGB 세트를 생성한다. 이후 정의 4를 기반으로 모든 FGB가 가장 가까운 FMB와 병합될 수 있는지를 평가한다. 병합이 성공하면, 데이터 커버리지를 향상시키기 위해 DM의 변화를 기반으로 병합된 FMB를 분할한다. 마지막으로, 알고리즘 5가 호출되어 각 FMB의 사전(dictionary) 구조를 스캔하고, 각기 다른 타임스탬프에서 온 데이터의 감쇠 값을 계산하며, 데이터를 비율에 따라 합산하여 WAV 값을 계산한다. 만료된 FMB는 제거된다.

D. 오프라인 단계

데이터 스트림을 클러스터링하는 과정에서, 클러스터의 개수와 모양을 예측하는 것은 도전적인 작업이다. 따라서, 오프라인 조건이 충족되면, 우리는 DPC(Density Peak Clustering) 알고리즘을 사용하여 클러스터링을 수행한다.

 

알고리즘 4: FGB와 FMB 병합

1. D가 남아 있는 동안, 알고리즘 2를 사용하여 FGB를 생성한다.
2. 각 fgb에 대해: 3. 식 12-14에 따라 MIR을 계산한다. 4. MIR이 1이면, fgb와 fmb를 병합한다. 5. **fmb.map[T]**에 fgb.num을 더해 업데이트한다. 6. DM에 따라 fmb를 분할하고 결과를 유지할지 결정한다. 7. MIR이 0이면, fgb를 fmb로 변환하고 FMBs에 추가한다.
3. 알고리즘 5를 사용해 WAV를 업데이트하고, 임계값 이하의 FMB를 제거한다.

알고리즘 5: WAV 업데이트 및 FMB 제거

1. 각 FMB에 대해: 2. W를 0으로 초기화한다. 3. 각 tkey에 대해:
   • W를 **fmb.map[tkey]**와 fmb.num의 비율에 따른 감쇠 값을 계산하여 업데이트한다
2. WAV 값을 계산한다.
3. WAV가 임계값보다 작으면, fmb를 FMBs에서 제거한다.

초기화 후, 우리는 FMB들의 집합을 얻게 된다. 알고리즘 4에서 설명한 바와 같이, 온라인 단계에서는 각 타임스탬프에서 들어오는 데이터가 알고리즘 2를 통해 처리되어 해당하는 FGB 세트가 생성된다. 정의 4에 기반해 모든 FGB가 가장 가까운 FMB와 병합될 수 있는지를 평가한다. 병합이 성공하면, 더 나은 데이터 커버리지를 위해 병합된 FMB를 DM의 변화를 기반으로 분할한다. 마지막으로, 알고리즘 5가 호출되어 각 FMB의 사전(dictionary) 구조를 스캔하고, 다른 타임스탬프에서 온 데이터의 감쇠 값을 계산한 후, 데이터를 비율에 따라 합산하여 WAV 값을 계산하고, 만료된 FMB를 제거한다.

 

알고리즘 6: DPC 기반의 FMB 연결

1. T가 오프라인 기준과 일치할 때:
2. list를 비어 있는 리스트로 초기화한다.
3. 각 fmb에 대해 fmb의 중심을 list에 추가한다.
4. list를 DPC 알고리즘의 입력으로 사용하여 각 fmb.center에 클러스터 라벨을 부여한다.
5. 각 fmb에 대해 동일한 라벨을 가진 fmb들을 같은 클러스터로 할당한다.

 

E. 시간 복잡도 분석

알고리즘 1에서는, 한 볼에 총 n개의 샘플이 있을 때, I는 볼 분할을 위한 최대 반복 횟수이며, d는 데이터의 차원수를 나타낸다. 볼 분할과 관련된 시간 복잡도는 FCM 알고리즘과 유사하며, 이는 O(4Ind)이다. 이후 자식 볼 사전(dictionary)을 구축하는 과정에서는 부모 볼 사전에서 키-값 쌍을 스캔하여 자식 볼 사전을 생성해야 한다. 그러나 이 단계에서 소요되는 시간은 볼 분할에 비해 무시할 수 있을 정도로 적다. 따라서 알고리즘 1의 전체 시간 복잡도는 O(4Ind)이다.

레마 2에 따르면, 알고리즘 2에서 N은 총 샘플 수, d는 각 샘플의 차원수, I는 볼 분할을 위한 최대 반복 횟수, k는 각 퍼지 그라뉼 볼에 있는 평균 샘플 수를 나타낸다. 알고리즘 2의 시간 복잡도는 [O(1), O((4I + 1)N d log2(N))] 범위로 계산된다. 평균 시간 복잡도는 O((4I + 1)N d log2(N/k))이다.

 

증명 2: 시간 복잡도 분석

먼저, 전체 데이터셋을 FGB로 간주한다. FGB를 두 개의 볼로 분할하는 시간 복잡도는 **O(4INd)**이다. DM과 DMweight를 계산하는 시간 복잡도는 **O(Nd)**이다. 따라서 첫 번째 분할 라운드의 시간 복잡도는 **O(Nd + 4INd)**이다. 이후 자식 볼을 추가로 분할하는 과정이 이어진다. 각 분할 과정에서 부모 볼의 샘플이 두 개의 자식 볼로 고르게 분포된다고 가정한다. 알고리즘 2의 시간 복잡도 도출 과정은 다음과 같다:

여기서 N/2^x는 최종적으로 얻어진 FGBs 내의 평균 샘플 수를 나타낸다. 최악의 시나리오에서는, N개의 샘플이 N개의 그라뉼 볼로 나뉘며, 각 퍼지 그라뉼 볼에 샘플이 하나만 포함될 수 있다. 이를 통해 시간 복잡도는 다음과 같다:

평균 시간 복잡도

평균적으로, 각 퍼지 그라뉼 볼에 포함된 샘플 수가 k인 경우, 알고리즘 2의 시간 복잡도는 **O((4I + 1)N d log2(N/k))**이다.

알고리즘 3에서 초기화 단계 동안 생성된 퍼지 마이크로 볼의 개수를 M이라고 가정하면, 알고리즘 3의 평균 시간 복잡도는 **O((4I + 1)N d log2(N/k) + M)**이다.

알고리즘 5는 WAV를 업데이트하고 FMB를 제거하는 과정을 설명한다. J개의 FMB가 있으며, 각각 평균적으로 t개의 시간 기간 데이터를 가지고 있다고 가정할 때, 알고리즘은 각 FMB의 사전 키-값 쌍을 스캔하여 WAV를 업데이트하고, 임계값보다 작은 FMB를 제거한다. 따라서 알고리즘 5의 시간 복잡도는 **O(J t)**이다.

알고리즘 4에서 각 시간에 도착하는 평균 데이터 수가 N_t라고 가정하면, 각 순간에 해당하는 데이터셋으로 FGB가 생성되고 FMB에 병합된다. 병합 후의 MIR 계산과 사전 업데이트 과정은 무시할 수 있다. 알고리즘 4의 시간 복잡도는 **O(J t + (4I + 1)N_t d log2(N_t/k))**이다.

마지막으로, 우리는 FMBs의 중심을 DPC 알고리즘의 입력으로 사용한다. 알고리즘 6의 시간 복잡도는 **O(J^2)**이다.

IV. EXPERIMENTS

우리는 GB-FuzzyStream 접근법을 평가하기 위해 합성 및 실제 데이터셋을 대상으로 심층적인 실험을 진행했다. 성능을 평가하기 위해 다른 스트림 클러스터링 알고리즘과 비교했으며, 모든 실험은 Windows 10 Professional 운영 체제에서 32GB RAM 환경에서 수행되었다. 클러스터링 성능을 평가하기 위해 세 가지 외부 기준을 사용했다: ARI(Adjusted Rand Index) [38], NMI(Normalized Mutual Information) [39], ACC(정확도) [40]. 각 데이터셋에서 특정 주기 T에 따라 결과를 평가하고 기록한 후, 비교를 위해 평균 값을 계산했다. 또한, 각 데이터셋에서 알고리즘의 전체 실행 시간을 기록하여 비교 방법의 효율성을 평가했다.

A. 데이터셋 설명

표 III은 실험에 사용된 데이터셋의 요약을 제공한다. 다음은 몇 가지 대표적인 데이터셋에 대한 간단한 소개이다.

1) 합성 데이터셋:

우리는 5개의 합성 데이터셋을 사용했다: DS1 [41], Banana1, DS H [41], RBF3, Benchmark2로, 이는 표 III에 표시된 주기적인 패턴에 따라 데이터 스트림으로 시뮬레이션되었다. DS1과 DS H는 가우시안 분포를 기반으로 한 복합 데이터셋이다. DS1에서는 시간이 지남에 따라 네 개의 클러스터가 2차원 공간의 중심으로 일정한 속도로 이동한다. DS H는 두 개의 클러스터가 3차원 나선형 패턴으로 이동하며, 두 번 교차하는 특성을 가진다. Banana는 개념 변화가 거의 없는 데이터셋으로, 전체 과정에서 겹침 현상은 한 번만 발생한다. RBF3는 40,000개의 샘플을 포함하며 상당한 양의 노이즈가 있다. 이 데이터셋은 처음에는 세 개의 뚜렷한 클러스터를 보이지만, 시간이 지남에 따라 클러스터가 병합되거나 분리되고, 사라지거나 새로운 클러스터가 생기며, 겹침 현상도 포함된다. Benchmark는 두 개의 안정적인 가우시안 분포 클래스를 가진 비정상 데이터 스트림으로, 세 번째 클래스는 다른 두 클래스 사이에서 이동하며 부분적으로 겹친다.

이 합성 데이터셋은 스트리밍 시나리오에서 개념 변화로 인한 클러스터 겹침 문제를 처리하는 알고리즘의 능력을 효과적으로 평가하기 위해 사용되었다.

2) 실제 데이터셋:

우리는 7개의 실제 데이터셋을 사용했다. 이 데이터셋들은 스트리밍 시나리오에 특화되어 설계되었다.

•  
• CoverType [42]: 이 데이터셋은 미국 산림 서비스의 지역 자원 정보 시스템에서 가져온 숲 덮개 유형에 대한 정보를 포함한다. 데이터셋은 서로 다른 숲 덮개 유형과 관련된 7개의 클래스 레이블로 구성된다.
• PowerSupply3: 이 데이터셋은 이탈리아 전력 회사에서 1995년부터 1998년까지의 시간별 전력 공급 데이터를 포함한다. 이 스트림의 개념 변화는 주로 계절적 변화, 날씨 조건, 하루 중 다른 시간에 의해 발생한다. 학습 과제는 현재 전력 공급이 하루 중 몇 시에 해당하는지를 예측하는 것이다.
• NOAA [43]: 이 데이터셋은 미국 해양 대기청에서 수집한 날씨 측정 데이터로 구성된다. 이 데이터셋의 개념 변화는 주로 온도, 풍속, 습도 등의 요인에 의해 발생한다. 학습 과제는 비가 올지 여부를 예측하는 것이다.
• GasSensor [44]: 이 데이터셋은 다양한 농도의 6가지 순수 가스에 대한 기록을 포함하며, 이는 센서 배열을 통해 분석된다. 농도 변화는 클러스터 이동을 유발하며, 이는 설치된 장치에서 통과하는 가스의 종류를 식별하는 데 어려움을 초래한다.
• ElectricDevices, StarLightCurves, Wafer: 이 데이터셋들은 UCR4에서 가져왔으며, 시간이 지남에 따라 기록된다. StarLightCurves 데이터셋은 천문학적 밝기의 시간 시계열을 기록한다. 이 데이터셋은 8,236개의 위상 정렬된 광도 곡선으로 구성되어 있으며, 각각 1,024차원의 데이터 포인트로 이루어져 있고, 이들의 카테고리는 전문가에 의해 결정된다. ElectricDevices 데이터셋은 영국 정부가 자금을 지원한 연구 프로젝트의 일환으로 만들어졌으며, 소비자가 가정에서 전기를 어떻게 사용하는지에 대한 데이터를 수집하여 탄소 배출량을 줄이는 데 도움을 주기 위한 것이다. Wafer 데이터셋은 칩 가공 중에 얻은 센서 측정값을 기록한 데이터셋이다.

B. 데이터 처리 및 매개변수 설정

실험 데이터셋에 대해 고차원 데이터 문제를 해결하기 위해 PCA(Principal Component Analysis) [45]를 사용하여 차원 축소를 수행하였다. 데이터셋의 각 샘플에 타임스탬프를 추가하여 이를 데이터 스트림으로 모델링하였다. 이후 수정된 데이터셋을 T 기간 동안 클러스터링을 위해 알고리즘에 입력하였다. 각 데이터셋의 구체적인 차원과 기간은 표 III에 자세히 나와 있다. 알고리즘의 성능을 공정하게 평가하기 위해, 우리는 제공된 원본 코드와 매개변수에 따라 알고리즘을 설정하여 비교 알고리즘의 정확한 모델링을 강화했다. GB-FuzzyStream에서는 ρ∗와 δ∗를 0.5로, m과 eps를 각각 2와 10으로 고정하였다. 데이터셋에 따라 λ 값은 0.2에서 2 사이, 임계값(threshold)은 0.3에서 0.8 사이로 설정하였다.

C. RBF3에서의 GB-FuzzyStream 시각적 표현

그림 5는 RBF3 데이터셋에서 GB-FuzzyStream의 세 개의 연속적인 시간 지점에서의 클러스터링 결과를 보여준다. t = 16에서 클러스터 3과 클러스터 4 사이에 부분적인 겹침이 관찰되며, 이후 분리되기 시작한다. 시간이 지나면서, t = 17에서 클러스터 3과 클러스터 4는 완전히 분리되고, 클러스터 3은 클러스터 2 방향으로 이동한다. 마지막으로 t = 18에서 클러스터 3과 클러스터 2가 가까운 거리로 인해 경계에서 부분적으로 겹치게 된다. 우리의 클러스터링 결과는 연속적인 개념 변화가 나타나는 일반적인 스트리밍 시나리오에서도 GB-FuzzyStream이 겹치는 경계를 가진 클러스터(예: 클러스터 3과 클러스터 4, 클러스터 2와 클러스터 3)를 성공적으로 감지하고, 클러스터의 개수를 정확하게 결정할 수 있음을 명확히 보여준다. 이는 GB-FuzzyStream이 그라뉼 볼 컴퓨팅 모델을 기반으로 퍼지 특성을 도입하여, 스트리밍 시나리오에서 데이터 겹침 문제를 해결하기 위해 퍼지 마이크로볼을 생성하기 때문이다.

D. 클러스터링 결과에 대한 논의

같은 데이터셋에 대해, 각기 다른 알고리즘들은 고정된 평가 기간을 가지며, 우리는 각 평가 기간 동안 ARI, NMI, ACC를 기록하였다. 표 IV는 평균 ARI, NMI, ACC 값을 보여준다. 전반적으로, GB-FuzzyStream은 대부분의 데이터셋에서 ARI, NMI, ACC 측면에서 다른 알고리즘보다 우수한 성능을 보이며 안정성을 유지하였다. 모든 비교 알고리즘 중에서, TSF-DBSCAN과 d-FuzzStream은 퍼지 특성을 도입하여 실제 스트리밍 시나리오에서 겹치는 클러스터 경계를 처리하는 데 뛰어난 성능을 보였다. TSF-DBSCAN에 비해 d-FuzzStream은 더 일관된 성능을 보였는데, 이는 오프라인 WFCM 과정에서 **예상 클러스터 수 kkk**를 실제 클러스터 수와 일치하도록 설정하여 d-FuzzStream의 올바른 모델링을 가능하게 했기 때문이다. MuDi-Stream, D-Stream, DenStream은 대부분의 데이터셋에서 경쟁력 있는 ARI 값을 내지 못했다. 반면, Chronoclust와 CEDAS는 퍼지 특성을 사용하지 않는 스트리밍 클러스터링 알고리즘 중에서 상대적으로 좋은 성능을 보였다.

1. 합성 데이터셋:
   • Banana 데이터셋의 경우, 평가 초기와 말기에는 클러스터가 하나이고, 중간 단계에서는 클러스터가 두 개로 겹침 현상은 없다. 우리는 d-FuzzStream에서 k 값을 2로 설정했기 때문에 성능이 낮아졌다. MuDi-Stream은 각 평가 창에서 과도한 클러스터 수를 생성하여 Banana 데이터셋에서 최악의 성능을 보였다. 겹치지 않는 시나리오에서는 GB-FuzzyStream과 TSF-DBSCAN이 잘 작동했다.
   • DS1 데이터셋의 경우, 모든 알고리즘이 잘 작동하여 서로 점점 가까워지는 네 개의 클러스터를 성공적으로 식별했다. 그중에서도 GB-FuzzyStream이 가장 좋은 결과를 얻었다. 이는 DS1에서 네 개의 클러스터가 끊임없이 이동하더라도, 겹치는 경계의 현상이 심각하지 않기 때문이다.
   • RBF3는 심각한 개념 변화 현상을 보이며, 이는 겹치는 클러스터 경계를 유발한다. 기존의 데이터 스트림 클러스터링 알고리즘과 비교했을 때, 퍼지 특성을 도입한 알고리즘들은 안정적인 성능을 보였다. 이는 소속도를 통해 경계 지점을 나누는 것이 겹침 현상을 완화하기 때문이다.
   • Benchmark 데이터셋에서는 세 개의 클러스터가 각 시간 창에서 나타나며, 하나의 클러스터가 다른 두 클러스터 사이를 오가며 번갈아 겹친다. d-FuzzStream은 각 평가 라운드에서 클러스터 수를 3으로 고정하여 가장 높은 ARI, NMI, ACC 값을 얻었고, GB-FuzzyStream이 ARI 값 측면에서 d-FuzzStream을 바짝 따랐다.
2. 실제 데이터셋:
   • StarLightCurves 데이터셋에서는 세 개의 클러스터가 동시에 나타나며, 두 개의 클러스터는 겹치고, 나머지 하나는 독립적으로 분포한다. d-FuzzStream을 제외하고, 다른 알고리즘들은 클러스터 수를 2 또는 4로 판단하였으며, 이는 실제 클러스터 수와 가깝다. GB-FuzzyStream이 가장 좋은 성능을 보였고, 다른 방법들의 성능은 비교적 비슷했다.
   • StarLightCurves 데이터셋에 비해, 다른 실제 데이터셋들은 심각한 개념 변화 문제를 가지고 있다. 특히 CoverType, PowerSupply, NOAA 데이터셋에서는 클러스터 간의 겹침 현상이 매우 심각하여 거의 모든 알고리즘의 성능이 저하되었다. 그러나, 우리의 알고리즘은 여전히 좋은 성능을 보였다.
   • 변화가 심한 GasSensor 데이터셋에서 GB-FuzzyStream은 실제에 가까운 클러스터 수를 생성하여 가장 좋은 성능을 보였다. 반면, DenStream은 과도하게 많은 클러스터를 생성하여 최악의 성능을 보였다.

E. 알고리즘 효율성 비교

표 V는 다양한 데이터셋에서 알고리즘의 총 실행 시간을 보여준다. 결과는 퍼지 개념을 도입한 새로 제안된 GB-FuzzyStream 알고리즘이 다른 퍼지 기반 스트림 알고리즘들에 비해 1~2 자릿수의 속도 향상을 달성했음을 보여준다. 이는 GB-FuzzyStream이 데이터 커버리지를 위해 다양한 그라뉼 볼의 크기를 생성할 수 있는 그라뉼 볼 컴퓨팅 모델을 사용하기 때문이다. 이 접근법은 온라인 및 오프라인 단계 모두에서 데이터를 거친 방식으로 처리할 수 있게 한다. 특히, GB-FuzzyStream은 d-FuzzStream보다 14.4배에서 267배까지 더 빠르며, TSF-DBSCAN에 비해 2배에서 90배까지 더 빠르다. 그러나, ChronoClust, CEDAS, MuDi-Stream, D-Stream, DenStream과 같은 비퍼지 스트리밍 클러스터링 알고리즘에 비해서는 실행 시간이 더 길다. 이는 GB-FuzzyStream이 클러스터 겹침 경계 문제를 해결하기 위해 퍼지 특성을 도입하여, 반복적인 소속도 계산이 필요하기 때문이며, 이는 추가적인 처리 시간을 소모하게 된다.

F. 민감도 분석

GB-FuzzyStream 알고리즘은 총 6개의 매개변수를 가지고 있다: λ, threshold, ρ∗, δ∗, m, eps. 우리는 FGB의 퍼지 분할 방법을 FCM 알고리즘에 기반하여 설계하였고, 퍼지 계수 매개변수 m과 반복 종료 매개변수 eps를 도입하여 각각 2와 10으로 설정하였다. **ρ∗\rho^*ρ∗와 δ∗\delta^*δ∗**는 오프라인 단계에서 사용되는 DPC 알고리즘에서 기원한 것으로, 클러스터 중심(밀도 피크)을 결정하는 데 사용되며, 이들 모두를 0.5로 설정하였다. 이러한 기반 위에서 사용자에게 중요한 매개변수는 λ와 threshold이다. λ 매개변수는 FMB의 감쇠율을 제어할 수 있으며, threshold는 현재 FMB를 제거할지 여부를 결정한다. 우리는 threshold를 0.3으로 고정하고, 평가 주기를 각각 1000과 400개의 샘플로 설정하여 개념 변화가 있는 RBF3 데이터셋과 정적인 StarLightCurves 데이터셋에서 λ의 민감도를 테스트하였다.

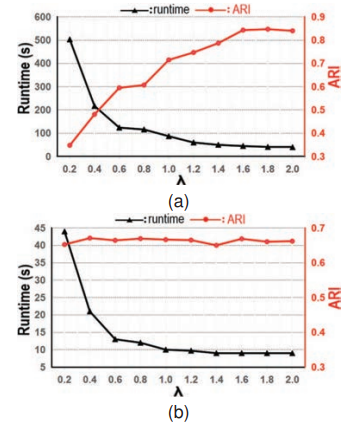
그림 6(a)에서 볼 수 있듯이, λ가 작은 경우, 알고리즘의 성능이 크게 저하되며 실행 시간이 증가한다. 이는 개념 변화 현상이 있는 RBF3에서 λ의 작은 값이 알고리즘이 만료된 FMB를 적시에 제거하지 못하게 하여, 많은 양의 역사적 데이터가 남아 심각한 데이터 겹침 문제를 야기하기 때문이다. λ가 증가함에 따라, 알고리즘의 성능이 안정화되는 경향을 보인다. 평가 기간에 남은 역사적 데이터가 없을 때, 알고리즘의 성능은 약간 감소한다. 실험을 통해, 평가 기간에 이전 기간의 소량의 역사적 데이터가 남아 있을 때, 알고리즘의 성능이 최적에 도달함을 발견하였다.

그림 6(b)에서 볼 수 있듯이, StarLightCurves 데이터셋처럼 개념 변화가 거의 없는 시나리오에서는 λ 매개변수의 민감도가 감소하며, λ 값의 변화는 알고리즘의 실행 시간에만 영향을 미친다. 이러한 정적 시나리오에서는 λ 값을 적절히 증가시켜 알고리즘의 효율성을 개선할 수 있다.

 

 

V. CONCLUSION AND FUTURE WORK

이 논문에서는 GB-FuzzyStream이라고 불리는 그라뉼 볼 컴퓨팅 모델을 사용한 효율적인 퍼지 스트림 클러스터링 방법을 제안한다. 우리의 접근법에서 주된 혁신은 데이터의 두 단계에서 거친(granular) 방식의 처리를 채택하고, 정확성과 효율성 요구를 충족하는 가중 감쇠 메커니즘을 통합한 것이다. 또한, 우리는 퍼지 기법을 스트림 클러스터링에 도입하고, 그라뉼 볼 컴퓨팅 모델을 사용하여 데이터의 적응형 퍼지 반복을 가능하게 했다. 이 접근법은 GB-FuzzyStream이 클러스터 경계 겹침 문제를 효과적으로 해결할 수 있도록 한다.

그러나, GB-FuzzyStream은 진화하는 데이터 스트림에 대해 사용자 친화적이지 않은 매개변수 설정이 필요하다. 향후, 우리는 알고리즘을 개선하여 적응형이면서 매개변수 설정이 필요 없는 방식으로 만드는 것을 목표로 할 것이다.