도미와 빙어를 구분하는 KNN모델을 만들려고 한다. 그런데 데이터의 형태에 따라 성능이 다르게 나오는 것을 다음의 과정들을 통해 알고 어떻게 성능을 높여 왔는지에 대해 작성할 것이다.
fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0,
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8,
10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0,
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7,
7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]다음과 같은 도미와 빙어의 데이터를 예로 들 것이다. 우선 이 데이터는 도미, 빙어 순으로 나열되어있는 것을 확인할 수 있다. 그런데 훈련셋과 테스트셋을 순서대로 자르면 훈련할 때는 도미만 훈련하고 테스트셋은 빙어만 있기 때문에 성능이 좋을 수가 없다.
이처럼 훈련셋과 테스트셋에 샘플이 골고루 섞여 있지 않으면 샘플링이 한쪽으로 치우쳤다는 의미인 샘플링 편향이 일어난다. 그래서 훈련셋과 테스트 셋을 나누기 전에 데이터를 섞거나 골고루 샘플을 뽑아서 훈련셋과 테스트셋을 만들어야 한다.
np.random.seed(42)
index = np.arange(49)
np.random.shuffle(index)
train_input = input_arr[index[:35]]
train_target = target_arr[index[:35]]
test_input = input_arr[index[35:]]
test_target = target_arr[index[35:]]이렇게 주어진 데이터의 index를 무작위로 섞은 다음 훈련셋과 테스트셋으로 나누는 코드이다.
그런데 이렇게 하면 또 다른 문제점이 생긴다. 무작위로 섞었을 때 운이 나빠서 한 종류의 데이터셋이 훈련셋이나 테스트셋에 많이 들어간다면 예측이 잘 되지 않는다.
그래서 사이킷런에서 제공하는 train_test_split()이라는 함수를 사용할 것이다. 이 함수는 전달되는 리스트나 배열을 비율에 맞게 훈련 셋과 테스트 셋으로 나누어 준다.(나누기 전에 알아서 섞음)
이제 테스트를 해보자.
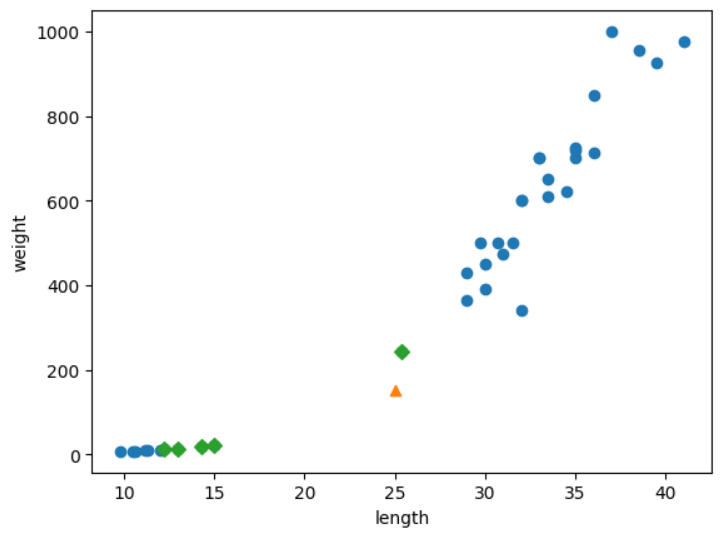
세모는 육안으로 봐서는 도미인 것 같다. 그런데 위의 코드 바탕으로 실행해보면 빙어가 나온다. 왜 가장 가까운 이웃을 빙어라고 생각한걸까? 이유는 가로세로 거리 비율에 숨어있다. 가로에 비해 세로의 범위가 너무 넓다. 그래서 y축으로 조금만 멀어져도 거리가 아주 큰 값으로 계산되는 것이었다.
이를 바로잡기위해 xlim()함수를 사용하자.
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')
plt.xlim((0, 1000))
plt.xlabel('length')
plt.ylabel('weight')
plt.show()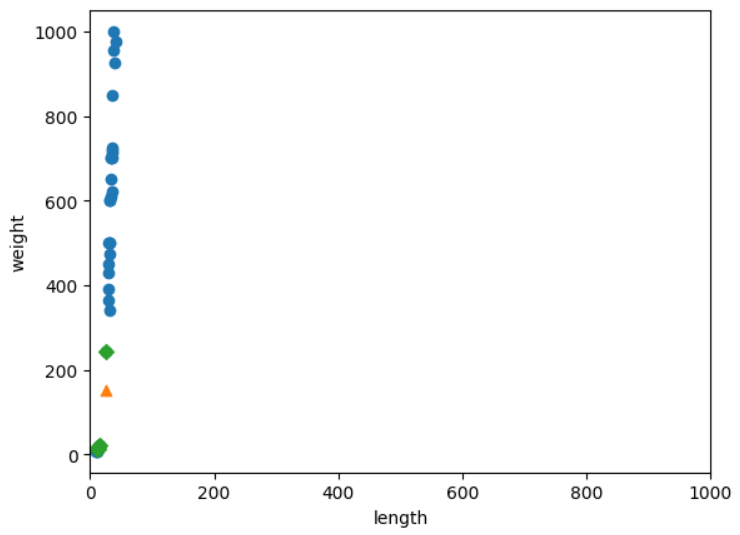
이런 데이터라면 x축은 가장 가까운 이웃을 찾는데 크게 영향을 미치지 못할 것이다!(해결)
이렇게 두 특성(길이, 무게)의 값이 놓인 범위가 매우 다른 것을 두 특성의 스케일이 다르다고도 한다. 데이터를 표현하는 기준이 다르면 알고리즘이 올바르게 예측할 수 없다. 이런 알고리즘(knn 포함)들은 샘플 간의 거리에 영향을 많이 받으므로 제대로 사용하려면 특성값을 일정한 기준으로 맞춰 주어야 한다. 이런 작업을 데이터 전처리라고 한다.
가장 널리 사용하는 전처리 방법 중 하나는 표준점수(또는 Z점수)이다. 표준점수는 각 특성값이 평균에서 표준편차의 몇 배만큼 떨어져 있는지를 나타낸다. 이를 통해 실제 특성값의 크기와 상관없이 동일한 조건으로 비교할 수 있다.
mean = np.mean(train_input, axis=0)
std = np.std(train_input, axis=0)
# 표준점수
train_scaled = (train_input - mean) / std
# 비교하려는 데이터도 mean,std를 이용해서 똑같이 변환
new = ([25, 150] - mean) / std
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
x축과 y축의 범위가 -1.5~1.5 사이로 바뀐것을 볼 수 있다. 훈련 데이터의 두 특성이 비슷한 범위를 차지하게 되었다. 이제 이 데이터셋으로 knn모델을 다시 훈련을 해보자. 훈련을 마치고 테스트셋으로 평가할 때는 주의해야한다. 평가할 셋을 훈련 세트의 평균과 표준편차로 변환해야 같은 비율로 산점도를 그릴 수 있다.
test_scaled = (test_input - mean) / std
kn.score(test_scaled, test_target)
distances, indexes = kn.kneighbors([new])
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.scatter(train_scaled[indexes,0], train_scaled[indexes,1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
이로써 특성값의 스케일에 민감하지 않고 안정적인 예측을 할 수 있는 모델을 만들었다.
'AI > 혼공파 머신러닝+딥러닝' 카테고리의 다른 글
| [ML 05-1] 결정 트리 (0) | 2024.05.15 |
|---|---|
| [ML 04-2] 확률적 경사 하강법 (0) | 2024.05.09 |
| [ML 04-1] 로지스틱 회귀 (0) | 2024.04.04 |
| [ML 03-3] 특성공학과 규제 - 릿지(Ridge), 라쏘(Lasso) (1) | 2024.03.31 |
| [KNN, ML 03-2] 선형회귀(Linear Regression) (0) | 2024.03.27 |